電磁気学は大学1〜2年で習う科目の中でも特に難しい
(単位が取りにくい)と思う。
私も落とした。
そこで、ここでの記事は1年生の時の私ぐらいのレベルを対象に
書こうと思っている。
私に単位が取れるように、また電磁気学が少しでもわかるように
するつもりで書いていく予定である。
最終的に、少なくとも教養レベルの電磁気なんて全然難しくないんだということを
示したいと思っている。
実際電磁気は難しくないと思うようになったけれど、
それを自分で説明するのはとても難しい。
どこまで良い記事を書けるかわからないが、
できる限りわかりやすくしていきたい。
電磁気学が1年生にとって特に難しいのは、まず
数学が難しいということがある。
電磁気学はベクトル解析を使って記述されるが、
これがかなり難しく、教官もあまりちゃんと説明してくれないので
なかなか理解できない。
そこで、ここでは「物理数学」のページに書いた
ベクトル解析の記事と照らし合わせながら読めるようにした。
ベクトル解析は難しくてできれば近づきたくない気がするが、
数学・物理系に進む人は必ず必要になるし、
わかってくると楽しいので電磁気を勉強する機会に一緒に
勉強するといいと思う。
「新イシカワ電磁気学」は、まず真空中のマクスウェル方程式を
目標として電磁気現象を考える。
まず静電磁場から入り、次に変動する電磁場について考えて
マクスウェル方程式を紹介する。
教養レベルの電磁気学(私の大学では「物理学A(電磁気学)」or「物理学B(電磁気学)」)
に対応できる程度まで扱う予定である。
先にマクスウェル方程式を紹介しておこう。
電磁気学にはいろいろな法則がたくさん出てきてわかりにくくなりやすいが、
とにかく一番大事なのはマクスウェル方程式である。
真空中のマクスウェル方程式(積分形)は以下のような形をしている。
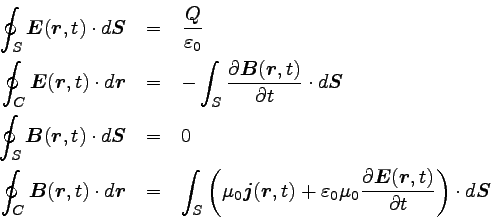
Eは電場、Bは磁場(磁束密度)を表している。
とりあえずは電気的要素、磁気的要素だと思ってもらえればいいと思う。
これから一つ一つ説明していくので、今はもちろんわからなくてよい。
ただ、これらと同じような式を見かけたら、それが重要であることを
注意するといいと思う。
電磁気学を実際に使うには積分形が便利なことも多いが、
実際にどういう法則かを考えたり、難しい問題を考えたりする場合には
微分系のマクスウェル方程式を考えた方がよいことが多い。
微分形は以下のような形をしている。
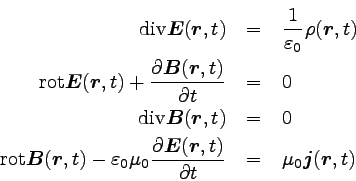
divやrotといったものが、先ほど触れた例の「ベクトル解析」の記号である。
divは「発散」と呼ばれる演算で、放射状に発生するイメージを
もつと良い。
rotは「回転」と呼ばれ、文字通り回転する要素に関することだと
考えてよい。
これらについては物理数学の項でもちゃんと説明するので、
とりあえずはイメージだけ持ってもらえばよい。
ρは電荷密度、つまりある点に存在する電気の量を表す。
jは電流密度、電流を表すベクトルだ。
∂/∂tは時間変化に関することを導いている。
これらのことから、マクスウェル方程式を眺めてみよう。
ε0、μ0は定数なのでとりあえず無視しよう。
一番上の式は、「電場」の「発散」=「電荷」となっている。
これは、電気のまわりに電気的要素が発生することを表す。
次は、「電場」の「回転」+「磁場」の「時間変化」がゼロとなっている。
これは、磁気的要素が時間変化すると電気的要素が回転して(渦状に)発生する
ことを示している。
3つ目は、「磁場」の「発散」はゼロという式。
磁気的要素は放射状に発生しないということを言っている。
最後は、「磁場」の「回転」−「電場」の「時間変化」=「電流」である。
磁気的要素が渦状に発生するのは、電流が流れたときか電気的要素が
時間変化したときであることを表している。
全部まとめて紹介したが、マクスウェル方程式を初めて見る人は
何のことだか全然わからなかったんじゃないかと思う。
それでも、とにかく教養レベルの電磁気学の目標が
これであることを頭の隅に置いておいて欲しい。
「新イシカワ物理学」では、全ての記事で基本的にSI単位系を
使用している。 電磁気学でもそれは同じなので、
MKSA単位系を利用して書いている。
他の単位系がどのようなものかはマクスウェル方程式を知らないと
わかりにくいと思うので、マクスウェル方程式の節で
簡単に説明した。 参考にしていただきたい。
「新イシカワ電磁気学」は、教養レベル以後の電磁気についても
記事を作成したいと思っている。
具体的には、真空中の電磁気学でまだ扱っていない個所、
物質中の電磁気学など
(私の大学の授業では、物理学科の「電磁気学1、2」に相当する)。
|
|

