電磁気学の中で最も基本的なのは静電気に関することがらである。
静電気といえば、下敷きで頭をこすると髪の毛が吸い付く現象などがある。
このような静電気的な力はクーロン力と呼ばれる。
この現象であるが、よく考えてみると凄い現象である。
なぜなら、下敷きでこすった髪の毛は重力に逆らって
上向きに吸い付くこともあるからだ。
つまりクーロン力は重力より強いということになる。
私たちが日常実感するのは重力だが、
実際に日常生活のスケールで一番重要な力は電磁気力である。
重力と電気の力を比べてみると、なんと電気の力のほうが
40桁近く強いのである!(本当は重力と電磁気力を直接「比べる」
ことはできない。 そこでここでは、重力と電磁気力両方の相互作用をする
もの、例えば電子に働く力で比較している。)
それでは何故日常的には重力の方が実感しやすいのかというと、
重力と電磁気力の重要な性質の違いがあるためである。
重力は引き合う力なので、重力により多くの粒子が集まって
地球のように大きなものが構成される。
その結果全体の質量が非常に大きくなるので、
力も日常的に感じられるというわけである。
一方、クーロン力には引き合う力(引力)と
反発する力(斥力)の両方が働く。
多くの場合これらが打ち消しあって、実感できるほどの
力は発生しないのである。
電気にプラスとマイナスがあることはご存知だと思う。
これらプラスやマイナスの電気は電荷と呼ばれ、
「プラスの電荷」「マイナスの電荷」などと表現する。
電荷をもっている粒子を、荷電粒子と呼んだりすることもある。
さらに、荷電粒子の大きさを無視して点として扱う場合、
その粒子を点電荷と呼ぶ。 点電荷は、単に電荷と
呼ばれることもあるので注意が必要だ。
原子は原子核と電子からなるという話は聞いたことがある人も
多いと思うが、原子核はプラスの電荷をもち、
電子はマイナスの電荷を持っている。
クーロン力は重力と違い引力と斥力が存在するのであった。
一般に、プラス同士、マイナス同士の電荷は
反発し合い、プラスとマイナスの電荷は引き合う性質を持っている。
重力が引力しかないので、質量にプラスマイナスは存在しない。
原子核と電子はプラスとマイナスの電荷をもっているので、互いに引き合っている。
同じ符号の電荷は反発しあうので、同じ種類の電荷ばかりが
一箇所に集まることは考えにくい。
プラスとマイナスの場合は引き合うが、この場合正味の電荷は
プラスとマイナスが相殺してゼロになってしまう。
よって、あまり大きなクーロン力が日常的に発生していないのである。
電荷は、プラスマイナスのほかに、どれだけ電気を
持っているかということも重要である。
これは電気量と呼ばれ(単に「電荷」ということもある)、
qという記号で表されることが多い。
電気量の単位はC(クーロン)である。 電気量の大きさが1クーロンである
マイナスの電荷は、
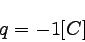 |
… (1) |
というふうに表す。 「電気量qを持つ荷電粒子」のことを、「電荷q」と表現することもある。
「電荷」という言葉は、電気自体、電気量、電気を帯びている粒子の3つのものを表すのである。
電荷の間に働く力は、それぞれの電荷に比例し(一つの電荷を倍にすると
力も倍になる)、電荷間の距離の2乗に反比例する
(距離を倍にすると力は1/4になる)。
二つの電荷をqおよびq’、距離をrとし、力をFとすると、この関係は以下のように表せる。
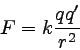 |
… (2) |
ただし、kは比例定数である。 (電気量)/(距離の2乗)は力の次元を持っていないので、
比例定数が必要になるのである。 この式はクーロンの法則と呼ばれる。
この式のように、ある物理量が距離の2乗に反比例する法則のことを一般に逆2乗則と呼ぶ。
qとq’が同じ符号ならば引き合い、違う符合ならば反発するので、
Fはプラスならば斥力、マイナスならば引力を表す。
比例定数kは定数なので、どのような形に書くのも自由である。
そこで、k=1/(4πε0)という形が使われている。
4πという部分が出てきて余計複雑になったように見えるが、
実はこうした方が後で計算が楽になる。ε0は真空の誘電率と呼ばれる
定数である(読み方は「イプシロン・ゼロ」)。
力は大きさだけでなく方向も重要である。
そこで力はベクトルで表される。 物理量をベクトルで表すことについては
物理数学の「ベクトル関数と微分」にまとめたので、慣れていない人は
こちらも参照していただきたい。 さて、力はベクトルで表されるということで、
クーロンの法則をベクトルを使って書き直してみよう。
電荷qのある位置ベクトルをr、電荷q’のある位置ベクトルをr’とすると、
電荷間の距離は|r−r’|である。
図示すると以下のようになる。
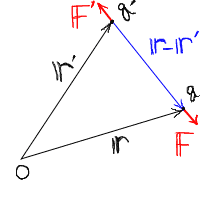 |
… (a) |
電荷qに働く力をFとすると、その力が働く方向は(r−r’)なので、
(r−r’)方向の単位ベクトル(r−r’)/|r−r’|
を先ほどの式にかければ力の方向を上手く表現することができる。
以上をまとめると、クーロンの法則は以下のように書くことができる。
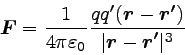 |
… (3) |
この式を見てみると、先ほどと違って力が距離の3乗に反比例しているような
印象を受けるかもしれないが、(分数の)分子の大きさが距離に比例しているので
正味逆2乗則になっている。
今度は、逆に電荷q’に作用する力F’を見てみよう。
F’も上の図に示してある。
これを求めるには、先ほどの式のrとr’を入れ替えればよい。 よって、
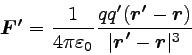 |
… (4) |
となる。 FとF’を見比べてみると、
大きさが同じで方向が逆、つまりF=−F’であることがわかる。
これは、作用・反作用の法則を表している。
空間に二つ以上の電荷があるときは、それぞれのクーロン力を
クーロンの法則に従って計算し、ベクトルの足し算をすれば
実際に働く力を求めることができる。 これは、力学での合力の計算がベクトルの
足し算で求めることができたのと同じである。 こういった性質は
重ね合わせの原理と呼ばれている。
以上が静電気の基本法則であるクーロンの法則の説明であるが、
なぜ逆2乗則になるか考えてみよう。 力が電気量に比例するのは
直感的にわかりやすいことである。 しかし、距離の2乗に反比例することは
少し直感的でないかもしれない。 まず、距離の何乗かに比例でなく
反比例する(rが分子でなく分母に来る)ことはあたりまえのことだろう。
力が距離に比例すると距離が大きくなるほど力が強くなってしまうが、それはおかしい。
反比例することは認めるとしても、2乗であるのはどうしてだろう?
ここで、先ほど導入した4πの要素が少し関係してくる。
分母にある4πと距離の2乗を組み合わせてみると、球の表面積4πr2の形を
していることがわかる。 電荷ひとつを固定してもう一つを動かして考えると、
力の大きさが同じになる場所は球面になっていることがわかるだろう。
そしてその球面は、距離が大きくなるほど4πr2に比例して
大きくなっていく。 力は、この球面が広がるにしたがって、その表面積に反比例して
弱くなっている(薄まってゆく)といえるのではないだろうか。
ただし、このことはクーロンの法則の解釈であって証明ではないので
注意が必要だ。 逆2乗則になるのは実験事実であって、
本当に厳密に正しいのかどうかはわからない。
電磁気学はクーロンの法則が厳密に逆2乗則であることを
仮定して成立している。
逆2乗則については、次に扱う「電場」という概念を使って考えた方がわかりやすい
かもしれない。
次のページでは、クーロンの法則を場の考え方から見てみることにしよう。
|
|
