前節では電荷間に働く力について扱った。
ここでは、クーロン力がどのようにして働いているかについて
少し考えてみよう。
クーロン力の伝わり方として、遠隔作用と近接作用の二通りの考え方がある。
遠隔作用というのは、電荷が互いに直接力を及ぼしているという考え方だ。
これは直感的には正しそうだが、どのように互いの電荷の
情報が伝わるのかということが説明しにくい。
一方、近接作用というのは、まず電荷が空間に影響を与え、
影響を受けた空間によりもう一つの電荷に力が働くという考え方である。
つまり、電荷が存在するだけでまわりの空間は普通の空間とは何か違うと考えるわけだ。
電荷から目に見えないオーラのようなものが出ていて、そのオーラがもう1つの
電荷を引っ張っているとイメージしてもらえばよい(ただしこのイメージには
少し語弊がある。これについては後述)。
これは非常に大胆な発想である。 しかし、遠隔作用の立場でも
電磁気の現象が説明できるとすれば、わざわざそんなことを考えなくても良い
と言えるかもしれない。
この2つの考え方には、実は大きな違いがある。
近接作用で予言される現象で、遠隔作用で説明できないものがあるのだ。
近接作用で考えた場合、電荷が1つしかない場合でも
空間は影響を受けると考えられる。
ここで電荷を動かすと、空間も変化するであろう。
さらに周期的に電荷を動かすとすると、空間に対する電気の影響が
波のように伝わっていくと考えられる。
このような波を、遠隔作用で説明できないような方法で
観測できれば、近接作用の方が正しいということが言えるだろう。
それでそのような波は観測されたのかというと、なんと光がそうだった
のである。 光の正体は電気及び磁気の波動現象だったのだ。
このような波は電磁波と呼ばれる。 電磁波には、人間の目に見える光(可視光)の他に
赤外線、紫外線、X線、電波が含まれる。
電磁波の存在が確認されたので、近接作用で考えていった方がよさそうだということが
わかった。
それでは、近接作用の考え方に従い電荷がまわりの空間にどのような
変化を与えるかを考えよう。 電荷により発生する、空間の電気的な
性質のことを電場(でんば)と言う(「電界」と呼ばれることもある)。
クーロンの法則により電荷が力を受けるとき、
その原因は電場であると考える。 そのため、電場はベクトル量であることが
わかる。 電場がベクトルでないと、電荷がどちらの方向に力を受けるかが
わからなくなってしまう。
電場はベクトルであり、場所によって違う値を持つ。
このようなベクトルは、ベクトル場と呼ばれる。
全空間中に矢印がびっしり詰まっているというイメージである。 電場中のプラスの電荷は、
その位置にあるベクトルの方向に、そのベクトルの大きさに対応する力を受ける。
マイナスの電荷の場合は逆方向に力を受けることになる。
ベクトル場については、物理数学のページの「スカラー場とベクトル場」にも
書いたので、そちらも参照していただきたい。
さきほど電場をオーラのようなものと表現したが、
これはベクトル場であることをイメージしにくい。
そこで、オーラの流れのようなものだと思ってもらえればよいかもしれない。
しかし電場は電場であってオーラではないのだから、以後は
この例えは使わない。 例えなしでも電場がイメージできるように
なっていただきたい。
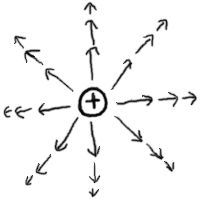
プラスの電荷による電場を図示してみると、以下のようになる。
 |
… (a) |
このように電場は等方的に広がっていて、その大きさは
電荷から遠ざかるほど小さくなる。
この図では2次元的に表現されているが、実際には3次元的に
全方向に向かって発生しているので注意が必要だ。
また、図示するためには矢印は有限個しか書けないが、実際には
全空間に対応するベクトルがあるということにも
注意しておかなければならない。
さて、r’の位置にある電荷q’が、位置rに
作る電場を式で表してみよう。電場をEとおく。
電場は位置rの関数なので、E(r)と書く。
近接作用の立場により、クーロン力は電場により電荷に作用すると考えるので、
クーロン力は電場と(力を受ける方の)電荷で表すことができる。
位置rにある電荷qに働く力をFとすると、
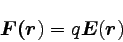 |
… (1) |
という関係になっている。 この式と前節で扱ったクーロンの法則の
式を見比べると、電場は
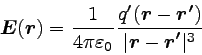 |
… (2) |
というふうに表されることがわかる。 クーロン力の場合に成り立った
重ね合わせの原理は、電場についても成り立つ。
つまり、複数の電荷からなる電場は、それぞれの電場を上の式のように
計算して足し合わせれば求めることができる。
電場を図示する方法には、上の図のような方法のほかに
「電気力線」(でんきりきせん)というものを使う方法がある。
電気力線とは、上の図の電場を表すベクトルをなめらかにつなげた線である。
例えば、プラスの電荷による電荷の電気力線は以下のようになる。
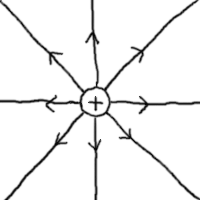 |
… (b) |
これは一見、確かに電場の様子がわかりやすいが、ベクトルをつなげてしまったために
電場の大きさがわかりにくくなっているように見えるかもしれない。
しかし、電場の強さは電気力線の密度から知ることができる。
電気力線が密集しているところでは電場が強く、逆に電気力線が疎なところでは
電場が弱い。
ここで再び注意しておきたいことは、図では8本の線が出ているが、
電荷から有限本の電気力線が出ているということを言いたいわけではない。
この図では、一見この8方向だけが特別に見えるかもしれないが、
そうではなく電気力線は3次元的全方向に等しく出ているのである。
電気力線にはいくつかの性質がある。 これらを定性的に
知っていればいろいろな電場の電気力線が描けるので、
電場の様子が予想できる。
まず、電気力線は電荷のないところでは発生・消滅しない。
プラスの電荷のあるところで発生し、マイナスの電荷のあるところで消滅する。
発生・消滅する電気力線の量は、その電荷の電気量に比例する。
これは、次節で紹介するガウスの法則による性質である。
次に、電気力線同士は反発しあい、電気力線自体は縮もうとするという
性質がある。 これは、マクスウェルの応力と呼ばれる性質である。
マクスウェルの応力はマクスウェル方程式が全て出揃わないと
説明できないのでここでは詳しく説明しないが、この性質を知っていると
電場がイメージしやすい。
以上のような性質から、プラスの電荷とマイナスの電荷が1つずつある
場合の電場の様子は以下のようになることがわかる。
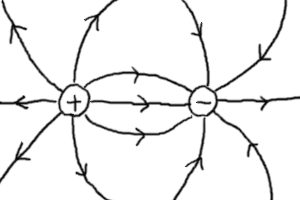 |
… (c) |
実際に電場がどのような数式で与えられるかは、それぞれの電場を
重ね合わせれば求めることができる。
前節で、クーロンの法則がなぜ逆2乗則であるかについて少し
触れた。 これは、電気力線で考えるとさらにわかりやすくなる。
電気力線は電荷からしか発生しないので、その密度は距離が離れるほど低くなる。
一つの電荷による電場は等方的に広がっていくので、密度は電荷を中心とする
球の表面積に反比例して小さくなってゆく。 よって、電場は4πr2に
反比例することがわかる。 電場とクーロン力は比例しているので、
クーロンの法則は逆2乗則になる。
これを一般化すると「ガウスの法則」に帰着する。 次節では、
このガウスの法則を詳しく見ていこう。
|
|

