前節では、クーロンの力が電場によって説明されることを見てきた。
さらに、電場は電気力線を使って図示するとわかりやすいのであった。
ここでは、電荷から電場が発生することを数式で表そう。
これは、ガウスの法則と呼ばれる静電気の重要な法則である。
ある有限の大きさの空間中から、どれだけ外向きに電場が出ているのかを
考えよう。 その空間の中に電荷がない場合、電気力線はその空間内で
発生・消滅しないので、入ってくる電気力線と出てゆく電気力線の量は
同じであると考えられる。 つまり、外向きに出て行く電場は正味ゼロである。
その空間内にプラスの電荷があれば電場は外方向に出てゆき、
マイナスの電荷の場合は内側に入ってくるだろう。
空間から外向きに出てゆく電場は、電場を閉曲面で面積分すれば
求めることができる。 面積分とは、ベクトル場を面に沿って積分することである。
ただし、面に対して垂直な成分のみ積分する。
詳しくは物理数学のページの「線積分と面積分」にあるので、参考にどうぞ。
さて、内側に電荷を含む閉曲面を面積分して、出てゆく電場の総量を
求めよう。 この閉曲面をSとする。 閉曲面での面積分は、数式では
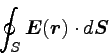 |
… (1) |
と表す。 dSは面積要素ベクトルと呼ばれるベクトルで、
大きさは微小面積、方向は面に垂直な方向というベクトルである。
面積分は、面積要素ベクトルとベクトル場の内積を取るので、
ベクトル場の面に垂直な成分のみを取り出すことができるのだ。
これから、この積分がどのような形になるかについて数学的に説明するが、
初めて見る場合は少し難しいかもしれない。 その場合は、
とりあえず飛ばして結果を見てもらっても構わない。
電荷は原点にあると考え、電気量はqであるとしよう。
電荷による電場は前節で扱ったとおりなので、それを上の面積分の式に
代入すると以下のようになる。
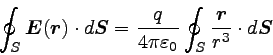 |
… (2) |
ただし、積分に関係ない定数の部分は、積分記号の外に出した。
(被積分関数)×dSを取り出して考えてみよう。
r・dSの部分は、内積なのでr×cosθ×dSと書ける。
ただし、cosθは面と電場のなす角である。 これを上の式に戻すと
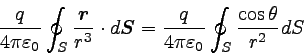 |
… (3) |
と書ける。 cosθdSの部分について
考えると、下の図にある部分の面積を表していることがわかる。
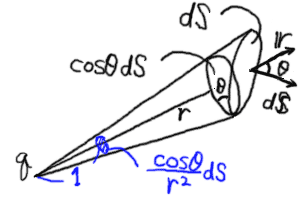 |
… (a) |
つまり、内積の計算により、電場の、面に垂直な成分が取り出されるのでなく、
面積の、電場に垂直な成分が取り出されると考えるのである。
このように、dScosθは位置ベクトルに垂直な微小面積であるということが
わかった。 それでは上の式にあるdScosθ/r2は
どうなるだろうか? dScosθは面積なので、
その大きさはr2に比例していると
考えられる。 これをr2で割ったものは、このような面の、
r=1のときの面積を表していると言える。
これは上の図の青で示した部分である。
積分により青色の面を全方向にわたって足し合わせるので、
積分の結果はr=1の球の表面積になる。 球の表面積は4πr2
なので、積分結果は4πになる。
以上から、閉曲面Sから外向きに出る電場の総量は以下のようになる。
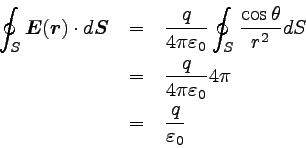 |
… (4) |
4πが相殺してなかなかすっきりした形になった。 クーロンの法則で
比例定数kを1/4πε0としたのは、このような形を得るためだった
のである。 この結果は、電気力線は電荷からしか発生・消滅しないことを
表している。 左辺の積分は、電気力線の立場から見るとSで囲まれた面内から
出る電気力線の総量と言える。 qがプラスのときは有限量の電気力線が
面から外に湧き出し、qがマイナスのときは面内に吸い込まれるというわけである。
さらに、その電気力線の量は電気量に比例する。 比例定数は1/ε0
である。
電荷による電場では、重ね合わせの原理が成立していた。
それを考慮に入れると、閉曲面内に複数個の電荷がある場合は、電場の面積分の結果は
その電荷を足し合わせた量になることがわかる。 閉曲面S内の電荷の総量をQとすると、
先ほどの結果から以下のように書ける。
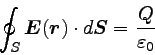 |
… (5) |
これがガウスの法則である。 ガウスの法則は、点電荷が複数ある場合だけでなく、
電荷が連続的に分布している場合にも成り立つ。 実際には
電荷は点電荷としてではなく金属などに連続的に分布して存在することが多い。
ガウスの法則における閉曲面Sは、ガウス面と呼ばれる。
ガウスの法則の凄いところは、閉曲面でありさえすればガウス面を
どのようにとってもよいということである。
ガウスの法則は、4つの式からなるマクスウェル方程式の1つである。
電荷がガウス面の外のみにある場合について考えてみよう。
先ほども触れたとおり、ガウス面内に入ってくる電気力線と出てゆく電気力線の量は
同じになる。 つまりガウスの法則の右辺はゼロになる。
よって一般の場合のガウスの法則の右辺は、ガウス面内にある電荷だけを足し合わせればよい
ことがわかる。
数学的には先ほどと同じように考えれば示すことができる。
ここではガウスの法則をクーロン力から導いたが、
実際にガウスの法則を満たす電場は、クーロンの法則による電場以外にも存在する。
つまり、ガウスの法則はクーロンの法則自体ではなく、
クーロンの法則を一般化したものであるといえる。
さらに電場が時間変化する場合にも成り立つという一般化をすると、
他のマクスウェル方程式と合わせて電磁波が予言される。
前述のとおり電磁波の存在は実証されたので、電場の時間変化まで考えた、
拡張されたクーロンの法則であるガウスの法則が成り立っている。
上に書いたガウスの法則は、ガウスの法則の積分形と呼ばれる。
「積分形」があるからには、「微分形」も存在する。
それもここで紹介しておこう。 実際の電場の計算は積分形だけで
できるので、微分形はまだほとんど使わないだろう。 だが、
マクスウェル方程式が出揃った時、微分形で書いたほうがいろいろな法則が
導き出しやすいので、微分形も重要である。
ただし、数学が少々難しくなるので、ここでは簡単に紹介するだけにとどめた。
ガウスの法則の微分形を説明するには、まず電荷密度ρ(ロー)について
説明する必要がある。 電荷密度とは、ある一点の電荷の密度を表す量で、
次元は[電荷]/[体積]である。
先ほど言った通り、電荷は連続的に分布している場合が多い。
そこで、電荷は電荷密度で表した方が良い場合が多い。
ある体積内に存在する電荷の総量は、その体積内にある
電荷密度を体積積分すれば求めることができる。 すなわち、
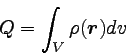 |
… (6) |
となる。
ガウスの法則の微分形を導くためには、ガウスの定理(ガウスの法則とは別物)が
必要になる。 これについては物理数学「ガウスの定理」参照。
ガウスの定理と電荷密度を用いてガウスの法則(積分形)の両辺を
体積積分の形に直すと、以下のようになる。
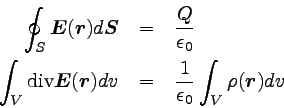 |
… (7) |
Vはガウス面Sで囲まれる空間のことを表す。
積分を同じ形にすることができたので、被積分関数が等しいといえる。
すなわち、
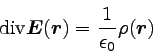 |
… (8) |
となる。 これがガウスの法則の微分形である。
divはベクトル場の湧き出しを表す微分演算で、ダイバージェンスと読み、
日本語では発散と言う。
これについても物理数学のページ「div(発散)」に書いたので、
必要になったら読んで欲しい。
あまり先に読んでしまうと混乱するかもしれないので、
積分形を使って静電気現象にある程度慣れてからにするとよいと思う。
ガウスの法則の微分形は、積分形と同じ内容の式である。
ただし、積分形が有限の大きさのガウス面を考えたのに対して、
微分形はある一点に対する法則である。
すなわち、ある一点から電場が発生するのは、その点の電荷密度による、
ということである。
次のページには、ガウスの法則(積分形)で電場を求める例を用意した。
ここの説明だけではまだイメージがつかめていないかもしれないと思うので、
例を通してガウスの法則を是非理解して欲しい。
|
|

