クーロンの法則からガウスの法則を導いてきたが、
クーロンの法則から静電場に関してもう1つ法則を導くことができる。
ガウスの法則は電場の面積分に関する法則であったが、
今回扱う法則は電場の線積分に関する法則である。
線積分とは、ベクトル場をある線に沿って積分することである。
ただし、線積分ではベクトル場の線と平行な成分のみを積分する。
線積分についても物理数学の「線積分と面積分」に書いたので、
必要ならば参照して欲しい。
ガウスの法則の時に閉曲面に関する面積分を考えたことをふまえ、
電場の、閉曲線に関する線積分を考えよう。 この閉曲線をCとする。
線積分は以下のように表せる。
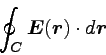 |
… (1) |
ただし、drはCに沿った微小なベクトルで、大きさは微小な長さ、
方向はCの接線方向である。
さて、この面積分の式の電場の部分に点電荷qによる電場の式
を代入して、この線積分がどうなるか考えてみよう。
電荷が原点にあるとすると、電場の式は
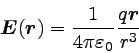 |
… (2) |
となるのであった。
よって、線積分は以下のように書き直せる。
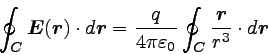 |
… (3) |
ただし、積分に関係ない定数は積分記号の外に出した。
これらの議論はガウスの法則のときと似ているのでわかりやすいと思う。
この積分のr・drの部分について考えてみよう。
r・drは内積なので、r×|dr|×cosθと書ける。
|dr|×cosθの部分は、r方向の微小な長さに相当する。
これをdrと呼ぶことにしよう。
図示すると以下のようになる(図のように|dr|とdrは異なることに注意)。
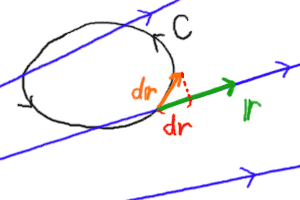 |
… (a) |
ただし|dr|×cosθは、θが鋭角になるか鈍角になるかによって
符号が変わる。 C上のr=rAからrBまで(往路)は
θが鋭角だとすると、残りの経路(復路)ではθは鈍角になり、|dr|×cosθは−drになる。
往路も復路もrに関する積分になり、rはrAからrBまで
変化する。
以上をふまえて線積分の式を計算すると、以下のようになる。
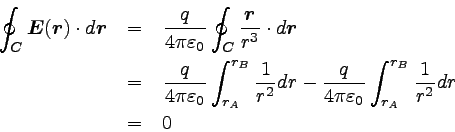 |
… (4) |
この結果は、渦状に回転する静電場が存在しないことを示している。
閉曲線Cに関する線積分がゼロでない値を持つ場合、ベクトル場には必ずCに沿って
回転している成分がなければならないからである。
上の式2行目第2項のrの積分範囲について、
復路はrがrBからrAへ変化するのだから積分範囲がおかしいと
思う人がいるかもしれない。 しかし、rBからrAに積分することの効果は
内積計算でマイナスが出たことにより、すでに使われている。
そのため、rの積分範囲は単純にrがいくつからいくつに変化するかということに
よって決めればよい。 ここで積分範囲をrBからrAまでにしてしまうと、
r=rBからrAまでの線積分とr=rAから
rBまでの線積分の値が同じになってしまう。
同じ積分を逆方向にすると符号が逆にならなければならないので、
おかしいことがわかる。
電場には重ね合わせの原理が成り立つことを考えて、この式はどのような電荷分布でも
成り立つと言える。 すなわち、任意の静電場に関して
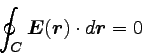 |
… (5) |
である。 ただし、この式はガウスの法則と違って電場(や磁場)が時間変化する場合には
必ずしも成り立たないので注意が必要だ。
上の法則が成り立つとき、電場の線積分は経路によらず一定であると言える。
このことを示すために、A点からB点までの線積分を考えよう。
AからBまでの経路として、経路1と経路2を考える。
上の法則により、A→1→B→2→Aという経路で線積分するとゼロになる。
よって、A→1→BとA→2→Bの線積分は等しい。
経路は任意に取れるので、線積分の結果は始点Aと終点Bの位置のみに
依存することになる。 このことから、この線積分に対する
「不定積分」を考えることができる。 AからBまでの線積分は、
不定積分の値にBの位置を代入したものからAの位置を代入したものを引けばよい。
電場に対する線積分の「不定積分」にマイナスをつけ、
以下のようなφ(ファイ)という量を定義する。
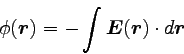 |
… (6) |
何故マイナスがつくかというと、電場の不定積分にマイナスをつけることにより、
この量が物理的意味を持つからである。
これがどういう物理的意味を持つかを説明する前に、性質を少し説明しよう。
まず、φは電位(でんい)と呼ばれる。 電位はスカラー場である。
なぜなら、線積分の結果を表したものなのでスカラー量であり、
場所によって違う値を持つからである。
スカラー場については物理数学の「スカラー場とベクトル場」参照。
電位の次元は[電場]×[距離]なので、[力]×[距離]/[電気量]である。
よって電場の単位は、ニュートン×メートル/クーロンであるが、
これには固有の名称があり、V(ボルト)と呼ばれる。
点電荷qが作る電位を実際に計算して、電位の意味を考えよう。
先ほどと同じように電荷は原点にあると考えると、
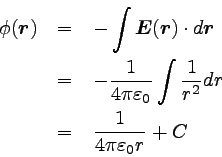 |
… (7) |
となる。 Cは積分定数である。 通常、電場の影響のないところでφ=0と
なるようにCを決める。 点電荷の作る電場の場合は無限遠で影響がなくなるので、
r→∞でφがゼロ収束するように、C=0とすることが多い。
点電荷のまわりに発生する電位は、電荷からの距離に反比例して
小さくなっていく。 このことを考えると、電場は
電位の高いところから低いところへの流れだと考えることができる。
これは、力学において、ポテンシャルエネルギーの高いところから
低いところに力が働くのに似ている。 そこで、電位は
静電ポテンシャルとも呼ばれる。 電場が電位の高いところから
低いところに発生する様子を数式で表すと、
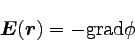 |
… (8) |
となる。 gradはグラディエントと読む微分演算子で、
スカラー場に作用してベクトル場を作る。
gradの演算により生成されるベクトル場は、
スカラー場の、値が小さい場所から大きい場所への流れを表す。
そこで、gradは日本語では「勾配」と呼ばれる。 スカラー場の
変化が急なほど、ベクトルの大きさは大きくなる。
電位の場合、電位の低い方に向かって電場が発生するので、
マイナスをつける必要があるということになる。
gradの具体的な演算方法などについては、物理数学の
「grad(勾配)」参照。
静電ポテンシャルをイメージでとらえると、
「高さ」に似たものである。 粒子は高いところから
低いところに力を受けるが、荷電粒子は静電ポテンシャルが
高いところから低いところへ力を受ける(荷電粒子がマイナスの電荷をもつ場合は
逆)。 ただし、高さとは違い、電位は3次元的に全空間に渡って
分布している量である。 だから、荷電粒子は電位の低い方向に
3次元的に、たとえそれが上方向であっても力を受けるのである。
2点の静電ポテンシャルの差を、「電位差」と言う。
これは、2点間の(電気的な)高さの差に対応する。
電位差のことを「電圧」とも言う。
さて、具体的に電位差の例を考えてみよう。
まず、ガウスの法則の例で少し触れた「面電荷」を考える。
ある導体面(面積S)に電荷が一様に分布していて、その電荷の総量はqとする。
面が十分大きいとすると、電気力線は面に垂直にしか
発生していないと考えることができる(端の様子が無視できるほど
大きい面を用意するということ)。
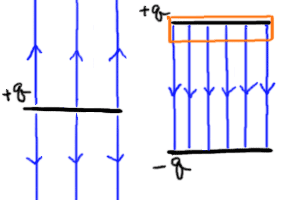
電気力線は下図の左側のように発生する。 このような面(極板と呼ぶ)を
2つ用意して、+qと−qに帯電させて平行に並べたものを
平行板コンデンサー(またはキャパシター)と呼ぶ。
極板間の距離はdとする。
 |
… (b) |
コンデンサー内の電場の様子は、上図右のようになる。
上下の極板からそれぞれ電場が発生するが、
重ね合わせの原理によりコンデンサーの外の電場はゼロになる。
よって、図にあるような電気力線で表される電場が発生していることになる。
この平行板コンデンサーの間の電位差を調べてみよう。
そのためには、まず電場の様子を知る必要がある。
平行板コンデンサー内の電場は、図のとおり一様であると
考えられる。 その大きさをEとして、ガウスの法則により電場を求めよう。
ガウス面、図のオレンジ色の部分をとると良い。
電場とガウス面は直行しており、電場が通る部分の面積は
極板の面積Sになる。 よって、電場は以下のように求められる。
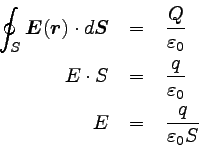 |
… (9) |
電位差を求めるには、電場を線積分すればよい。
今、図において電気力線はプラスの極板からマイナスの極板に向かって発生しているので、
プラスの極板の方が電位が高いことになる。
その差をVとすると、
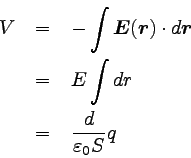 |
… (10) |
となる。 Vには電位の定義からマイナスが付くが、
マイナスの極板からプラスの極板に向かって積分しているので、
E・drがマイナスになり、相殺している。
Eは先ほど求めたとおり定数なので積分には関与しない。
drの積分は極板間の距離に相当するのでdになる。
よって、上の式にあるように電位差を求めることができた。
今行った計算は、電位が小さいところから大きいところへの
線積分であった。 しかし、結局マイナスの符号が相殺し、
電場に沿った積分になった。 このように、電位差を求める場合には
単に電場に沿って線積分するだけでもよい(この場合積分の前のマイナスは
つけない)。
この平行板コンデンサーに対して、電荷qが与えられていると
考えて電位差を求めたが、実際には極板に決まった電荷を与えることは難しい。
逆に、電位差を人為的に作り出すことは可能である。
例えば、電池は1.5Vなどの電位差を作り出す装置である。
今まで扱ったのと逆に、平行板コンデンサーに電位差を与えると、
両極板にプラスとマイナスの電荷が集まる。
コンデンサーとは、このように電位差により電荷を集める
装置のことである。
コンデンサーの能力は、ある電位差をかけたときに
どれだけの電荷が集まるかによって評価される。
この能力は静電容量と呼ばれ、Cという記号で表されることが多い。
静電容量の単位はF(ファラド)である。
1ファラドのコンデンサーに1ボルトの電位差を与えると
±1クーロンの電荷が極板に集まるので、Q=CVの関係があることがわかる。
平行板コンデンサーの場合、
Vとqの関係は先ほど求めたとおりである。
これとQ=CVを比較して静電容量を求めると、
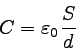 |
… (11) |
となることがわかる。 極板の面積が大きい場合や
極板間の距離が小さいほど静電容量が大きく、
より多くの電荷を集められることがわかる。
静電場に関して、ガウスの法則と、一周線積分がゼロになるという
2つの法則を紹介した。 静電場に関する基本法則は
この2つで、後はこの法則をどう使っていくかの問題である。
次節では、平行板でないコンデンサーの例を用意した。
今回の例でもおわかりいただけたと思うが、コンデンサーの問題は
静電場に関する両方の法則が必要になる。
次節のれいによって、
静電場の2法則の理解を深めて欲しい。
|
|

