静電場に関する2つの法則から、同心球コンデンサーの静電容量を求めてみよう。
まずは静電場の2法則の復習から。
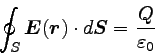 |
… (1) |
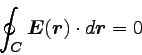 |
… (2) |
上の式はガウスの法則で、電場の源は電荷であることを表している。
下の式は、電場の回転成分が存在しないこと、つまり閉曲線になる電気力線が
存在しないことを示している。 この下の式の性質から、電場の「不定積分」である
静電ポテンシャル
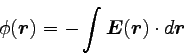 |
… (3) |
が定義できるのであった。
同心球コンデンサーとは、大小2つの球殻の導体からなるコンデンサーである。
ただし、二つの球の中心は一致している。 それぞれの球の半径をa、bとしよう。
ただし、半径aの極板が内側(つまりa<b)であるとする。
図示すると以下のようになる。
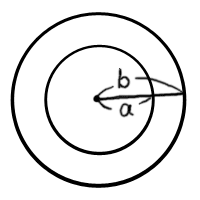 |
… (a) |
図では円形にしか描けないが、実際は球の中に球が入っている構造である。
コンデンサーの静電容量を求めるには、まずガウスの法則により電場を計算し、
電場を線積分して電位差を求め、Q=CVからCを求めればよい。
実際には電圧Vを与えたときにどの位電荷が集まるかを示すのが静電容量であるが、
静電容量を求めるためには、逆に電荷が与えられたときの電位差を
求めればよいのである。
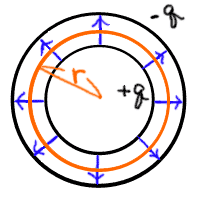
それではまずガウスの法則から電場を求める。 内側の球にq、外側の−qの電荷が
集まっているとする。 すると、電場の様子は以下のようになると考えられる。
 |
… (b) |
球の間以外ではガウスの法則により電場はゼロになる。
球の間での電場は、球の中心から放射状に出ている。 これを
ガウスの法則を使って求めよう。 ガウス面には、上の図のオレンジの部分のような
球面をとると良い。 この球の半径をrとする。
このガウス面は常に電場と直交しているので、ガウスの法則の左辺は
E×(球面の面積)になる。 よって、電場の大きさは以下のように計算できる。
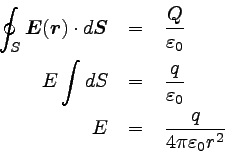 |
… (4) |
電場の方向はr/rである。 以下の計算では電場の大きさしか
使わないが、電場はベクトル場であることを常に意識していないといけない。
電気力線の様子から、内側の球のほうが電位が大きいことがわかる。
そこで、2つの球の電位差を求めるために、外側の球から内側の球に向かって
線積分する。 ただし、電気力線に沿って積分するものとする。
こうすることにより、線積分の中身E・drのEと
drが平行になるので計算しやすくなる。
ただし、これらは逆方向になるので内積の結果は−Edrになる。
rはaからbまで変化する。
以上から、電位差の計算は以下のようになる。
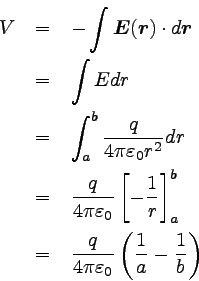 |
… (5) |
この式でのrの積分範囲について、前節(前半)と同じことが言える。
すなわち、外側から内側までの積分であっても、
rの積分範囲は単純にrがいくつからいくつに変化するかということに
よって決めなければならないということである。
外から内側に向かって積分している効果は、内積でマイナスが
出たことによりすでに使われているのである。
前節後半のコンデンサーの所で説明した通り、電位差を求めるには
単に電場に沿って(マイナスの符号をつけずに)線積分するだけでもよい。
そのほうが今の話のようなことを考えなくてもよいので
混乱しなくて良いかもしれない。
これで電荷と電位差の関係を求めることができた。
これとQ=CVを比較すれば静電容量を求めることができる。
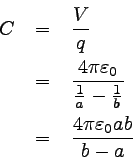 |
… (6) |
以上のように静電容量が計算できた。 具体的に数字を入れてみればわかるが、
平行板コンデンサーと同じように電荷間の距離が近い方が
静電容量は大きくなる。
ただし、距離がゼロになるとプラスとマイナスの電荷が混ざって
中性になってしまい、コンデンサーの役割を果たさなくなる。
これで静電場については終わりで、次からは磁場の話題に入る。
次節では、電場におけるガウスの法則に対応する
法則を説明する。
|
|

