前節から磁気を扱っているが、現実には磁石よりも
荷電粒子にどのように磁場が影響を及ぼすかのほうが重要になる。
ここでは、磁場により荷電粒子に働く力を示し、
一様な磁場中で荷電粒子がどのように運動するかを紹介する。
荷電粒子は電場により力を受ける。
これが近接作用の立場であった。
磁極は磁場により力を受けるが、荷電粒子も磁場により
力を受ける。 電気的な現象と磁気的な現象は
さまざまな相互作用を起こす。 そういうわけで「電気学」「磁気学」と
分かれないで「電磁気学」として一緒に扱う必要が出てくるわけだ。
それでは、実際に磁場中の荷電粒子に働く力を見ていこう。
電場に対して電荷qは、F=qEの力を受けるのであった。
電荷が電場により受ける力は電場と同じ方向である。
これに対して電荷が磁場により受ける力は、磁場に垂直な方向である。
この力を数式で表すと以下のようになる。
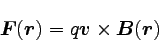 |
… (1) |
qは電荷の電気量で、vは電荷の速度ベクトルである。
磁場による電荷への力は、電荷が動いていないときにはゼロになる。
電荷が動いているとき、磁場と運動方向に垂直な方向に力が働く。
右辺のベクトル同士の掛け算は外積である。
外積はベクトル同士の演算で、結果もベクトルになる。
外積の結果得られるベクトルは、元の2つのベクトルそれぞれに
垂直な方向になる。
外積については物理数学の「内積と外積」参照。
電場と磁場の両方がある場合は、荷電粒子はこれらの力の合力を
受けることになる。 式で表すと以下の通り。
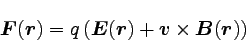 |
… (2) |
これは電磁場が電荷に作用する力の一般的な形で、
このような力のことをローレンツ力と呼ぶ。
電場による力は止まっている粒子にも働くので、
電場は粒子に(力学的)仕事をすると言える。
これに対し磁場による力は、粒子が運動しているときのみに働き、
その方向は常に粒子の運動に垂直な成分なので、
粒子の運動方向を変えるだけで仕事をしない。
この式からもう1つ非常に重要なことがわかる。
すなわち、磁束密度と電場との次元の関係である。
磁束密度の単位は[T]=[Wb/m2]で、
電場は[N/C]であった。
前に導入したボルトという単位を使えば、
[V]=[J/C]であるので、
電場は[V/m]と書くこともできる。
ローレンツ力の式によると、
電場と磁束密度は速度だけ次元の違いがある。
すなわち、磁束密度は[T]=[V/m]/[m/s]=[V・s/m2]
と表すことができる。
ここから、磁束の単位[Wb]は[V・s]であることもわかる。
ただし、これらは全てSI単位系の場合である。
SI単位系でない場合については「
マクスウェル方程式」に書いたので、
参照していただきたい。
一様な磁場中で、荷電粒子の運動がどのようになるか
考えてみよう。 磁場はz方向に一様で、磁束密度の大きさはBとする。
時刻t=0において、電気量qを持つ荷電粒子がy方向に速さvで
運動していたとしよう。 すると、t=0では
粒子はx方向にqvBの大きさの力を受ける。
力を受けても磁場は仕事をしないので、速さは変わらない。
粒子はxy平面上を運動し、粒子の進行方向と磁場は常に
直交するので、力の大きさは常にqvBである。
また、粒子は常に進行方向に対し垂直に(z方向を上と考えて)右側に
力を受ける。 このような粒子は、円運動すると言える。
図示すると以下のような様子である。
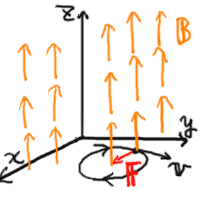 |
… (a) |
電荷がプラスだと図のように時計回りに運動するが、
マイナスの場合反時計回りに運動する。
このような、一様磁場中の荷電粒子の円運動は
サイクロトロン運動と呼ばれる。
円運動をすることがイメージできない場合は、実際に運動方程式を
解いてみると良い。
磁場は仕事をしないので、粒子の速さは常にvである。
粒子の質量をm、運動の半径をrとすると、
等速円運動の一般的性質から向心力はmv2/r
となる。 実際に働いている力はローレンツ力であり、
その大きさはqvBであった。 これらの2つが等しいことから、
この円運動の半径は
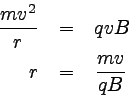 |
… (3) |
となる。 速度や質量が大きいと円運動の半径は大きくなるが、
電気量や磁場が大きいと半径は小さくなる。
また、角振動数ω(オメガ)は一般にv/rと書けるので、
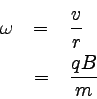 |
… (4) |
と求められる。 これはサイクロトロン運動に
特徴的な量で、サイクロトロン角振動数と呼ばれる。
サイクロトロン運動は、加速器(粒子を加速し衝突させる実験装置)
に利用されている(サイクロトロンとはこの加速器の名称である)。
磁場中の荷電粒子に実際に力が働く例としてサイクロトロン運動を
紹介したが、これはあまり日常的な現象ではないかもしれない。
次節では、電流の話題に入る。 電流間に働く力
もローレンツ力により説明される。
|
|

