この節では、電流の作る磁場について説明する。
小中学校で、電流の周りで方位磁石が動くということを
習ったのを覚えている人も多いだろう。
ここでは、このことを数式を使って定量的に説明する。
静電場のところでは電荷について説明したが、
ここで電流について説明する。
電池を回路につなぐと電流が流れるということは
誰もが知っているだろう。 このとき回路内では
何が起こっているのだろうか?
電池とは電位差を与える装置であるということは
「静電ポテンシャルとコンデンサー」の
コンデンサーの説明のところで少し触れた。
電位差を与えると電場が発生する。
電場が発生すると、荷電粒子はF=qEにしたがって
力を受ける。
物質は原子核(プラスの電荷を持つ)と電子(マイナスの電荷を持つ)で
できているので、それぞれ電場により力を受ける。
絶縁体中では、原子核と電子は強く結びついているので、
電場により力を受けても原子核と電子は互いに結びついたまま
である(しかし全く電場の影響を受けないわけではない。このことについては
「物質中の電磁気学」として記事を作成予定)。
しかし導体中では、原子核との結びつきが弱い電子が存在する。
このような電子は自由電子と呼ばれ、電圧がかかると
導体中を電場にしたがって自由に(原子核に束縛されずに)運動する。
電流とは、このように電荷が移動している現象のことである。
ある面を単位時間に横切る電荷をIとするき、その面に電流Iが
流れていると言う。 電荷の単位はSI単位系ではA(アンペア)で、
1Aは1秒間に1Cの電荷が移動する時の電流である。
このような定義のため、電流はスカラー量である。
電子の電荷はマイナスなので、電流と電子の流れは逆方向になる。
電荷が2つあるとその間にはクーロン力が生じたが、
2つの電流が平行に存在すると、それらの間にも力が生じる。
この電流間に働く力はアンペール力と呼ばれている。
電流同士が互いに同じ方向に流れている場合は引力、
逆方向に流れている場合には斥力が生じる。
この力はそれぞれの電流に比例し、電流間の距離に反比例する。
よって、アンペール力は以下のような式で表すことができる。
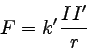 |
… (1) |
それぞれの電流をIおよびI’、電流間の距離をrとした。
k’は比例定数であり、クーロンの法則の比例定数kと
混同しないようにk’とした。
Fは力であるが、電流間の力であるので一点に働く力ではなく、
電流という線上に均等に働く力である。
そのため、ここでのFは単位長さあたりに働く力であり、
次元は、[力]/[長さ]である。
平行な2つの電流は上下に流れているとして、上向きに進む電流をプラスとする。
電流の向きが同じ場合は電流の符号が同じになり、Fはプラスになる。
これは引力を表している。
逆に電流の向きが逆の場合はFはマイナスになる。 これは斥力である。
比例定数k’は、SI単位系ではμ0/2πという形を
使う。 μ0は真空の透磁率と呼ばれる定数である。
よって、アンペール力は以下のように書き直せる。
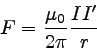 |
… (2) |
2πという因子は、ガウスの法則のときと同じように、
後で導かれる法則の形がきれいになるように導入されている。
静電場を導入したときに、近接作用の考え方について
説明した。 近接作用では電荷は直接的に力を及ぼすのではなく、
電場によって間接的に力を説明するのであった。
電流に働く力についても、直接的に力が働いているとは
考えずに近接作用により考えてみよう。
まず考えられるのは、電流のまわりに電場が発生しているということである。
電流は電荷の移動であるので、確かに電流の中に電荷が存在する。
しかし、電流中には自由電子のほかに、動かない原子核が存在する。
それらの電荷の総量はゼロになっているので、ガウスの法則により
電場は発生していないと言える。
そこで考えられるのが磁場である。 電流のまわりに磁場が発生していて、
その磁場により電子がローレンツ力を受けていると解釈できるのである。
磁場によるローレンツ力はF=qv×B
だったので、v、B、Fが右手系をなす
(右手を「フレミングの法則」の形にしたときに親指がv、
人差し指がB、中指がFの方向になる。
物理数学の「内積と外積」参照)。
両方の電流が画面上にあり、上に向かって流れていると考えた場合、
vの方向は上方向になる。
この場合発生するアンペール力は引力で、右側の電流は左側に力を
受けることになる。
ということは、右側の電流にはたらく原因になる磁場は画面の奥のほうに向かって
発生していることになる。 以上を図示すると以下のようになる。
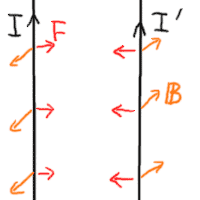 |
… (a) |
右側の電流に作用している磁場は左側の電流が作ったもので、
左側の電流に作用している磁場は右側の電流が作ったものである。
磁場はそれぞれ画面向かって奥、および手前に向かって発生している
(それを平面上に表現するのは難しい!)。
さて、電流による力とアンペール力から、磁場は上のように発生している
ことがわかった。 近接作用の立場では、電流が1つしかなくても
磁場は発生する。 それでは電流から発生する磁場はどのような方向を
向いているだろうか? 上の電流間に働く力の関係から考えて、
右ネジの方向に磁場が発生していると考えられる。 右ネジの方向とは、
ある方向に向かってネジを締めるときに回転させる方向である。
この場合はネジの方向は電流の方向である。
画面の奥から手前に向かって流れる電流の作る磁力線を図示すると、
以下のようになる。
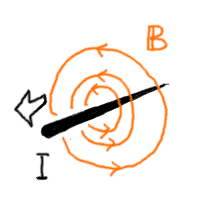 |
… (b) |
電流に近い方が磁力線が密集しているが、これは電流に近いところの方が
磁場が強いことを表している。
電流から発生する磁束密度の大きさについて考えよう。
これは上のアンペール力の式とローレンツ力の式から求めることができる。
まず、ローレンツ力は速度vで動いている荷電粒子の運動に
関する式だったので、これが電流に対してどのように働くか
考えなければならない。 逆に、1mあたり電荷qが動くときに
どれだけの電流が流れるか考えてみよう。
電流の速さをvとすると、1秒間に電荷はvメートルだけ移動すると考えられる。
よって電線に垂直な面を横切る電気量は1秒間にqvクーロンであると考えられる。
すなわち、I=qvである。
ローレンツ力の式について、大きさだけ考えるとF=qvBとなるので、
F=IBという関係がわかる。 これとアンペール力の式を比較すると、
電流のまわりに発生している磁束密度の大きさは
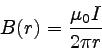 |
… (3) |
となることがわかる。 このように、電流の回りには磁場が発生し、
その磁場が電流にF=IBという大きさの力を与えることがわかる。
直線電流により発生する磁場はこのように求められたが、
これは無限に長い直線電流により発生する磁場なので、
他の形の電流には応用しにくい。
そこで、直線電流の周りの磁場の式を一般化した法則を導こう。
これはアンペールの法則と呼ばれ、
定常電流(電流自体が時間変化しない場合)に対して
一般に成り立つ法則である。
電流による磁場は、上の図にあったように
右ネジの方向に発生するのであった。
このように、電流により閉曲線の磁力線が発生する。
このような回転成分は静電場には存在しないことを
「静電ポテンシャルとコンデンサー」
のところで説明した。
静電場の場合は回転成分がないことは、閉曲線での
線積分がゼロになることから示した。
磁場の場合も閉曲線で線積分することにより、
回転する磁場がどのように発生するのかを考えることができる。
閉曲線で磁束密度を線積分する。 数式では、
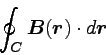 |
… (4) |
と表すことができる。
磁束密度には、上で求めた直線電流の磁束密度を代入して
この積分の結果がどのようになるか考えてみよう。
閉曲線Cには、直線電流を囲む任意の線を取る。
積分の方向は電流に対して右ネジの方向とする。
直線電流は原点を通るものとする。
磁束密度はベクトル場なので、方向も考える必要がある。
磁束密度の発生する方向は右ネジの方向であったので、
この方向の単位ベクトルeBで表す
ことにする。
すなわち、B=BeBとなる。
これを線積分の式に代入すると、
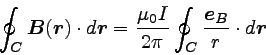 |
… (5) |
となる。 ただし、積分に関係ない定数は積分記号の外に出した。
積分記号の中のeB・dr/rについて
考えてみよう。 まず、eB・drは
内積なので、微小ベクトルdrのeB方向成分、
すなわち右ネジの方向成分の長さ(正射影)になる。
図で表すと以下のようになる。
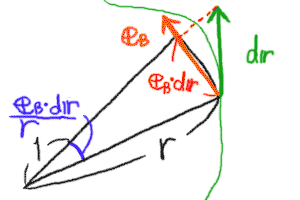 |
… (c) |
この長さは、半径rの扇形の弧の微小長さに相当する。
eB・dr/rは、さらにこれをrで割るので、
半径1の扇形の弧の微小長さになる(青い部分)。
半径1の扇形の弧はその角度(ラジアン)に対応するので、
この積分は角度を1周分積分することになる。
よって、その結果は2πとなる。
以上のことを元の式に戻すと、
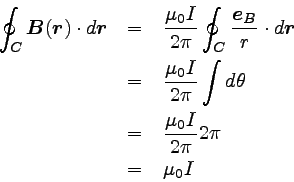 |
… (6) |
となる。
導かれた結果は、
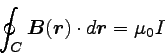 |
… (7) |
というものである。
この結果は、磁場の回転成分は電流によって発生することを
示している。 これはアンペールの法則と呼ばれる。
磁場に関しても重ね合わせの原理が成り立つので、
電流が複数通っている場合でもこの法則は成り立つ。
そのような場合は、右辺の電流の部分を閉曲線C内を通る
全電流と考えればよい。
ただし電流の符号は、電流の右ネジの方向がCと一致する場合はプラス、
逆になる場合にはマイナスにとらなければならない。
アンペールの法則は、直線電流以外の電流でも成り立っており、
アンペール力の説明を一般化したものである。
他の形の電流が作る磁場に関しても
アンペールの法則は成り立つということがわかっているので、
電流による磁場を求める際にはこれを利用することができる。
ただし、電流が時間変化する場合にはこの法則は
必ずしも成り立たなくなるので注意が必要だ。
ここまでではまだ静電場・静磁場しか扱っていない。
時間変化する電場・磁場まで考慮したときにマクスウェル方程式の
全てが揃い、多くの電磁気的現象を扱うことができるようになる。
上で求められたのはアンペールの法則の積分形で、
実はアンペールの法則にも微分形が存在する。 ここでこれを紹介しておこう。
そのためには、電流密度というベクトルを導入する必要がある。
電流は、有限な大きさの面を横切る電気の量であるので、
方向が重要になるにもかかわらずベクトルで表すことができない
(面の大きさが有限なので方向が定まらない)。
これに対し、電流の一点における密度は、無限小の面を
横切る電気の量であるので、ベクトルで表すことができる。
このようなベクトルは電流密度とよばれ、jで表す。
電流密度の次元は[A/m2]となる。
電流密度は微小面を通る電流であるので、これを
有限の大きさの面で面積分すれば電流になる。 すなわち、
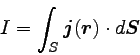 |
… (8) |
という関係が成り立っている。 この式とストークスの定理という
式を利用すると、アンペールの法則の微分形を求めることができる。
ストークスの定理については、
物理数学の「ストークスの定理」参照。
ストークスの定理および電流密度を用いて、アンペールの法則を以下のように
面積分の形に書き直す。
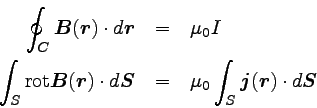 |
… (9) |
面積分の範囲Sは閉曲線Cが囲む任意の面である。
同じ形の積分の値が等しいという式になったので、
被積分関数が等しいと言える。 すなわち、
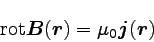 |
… (10) |
となる。 これがアンペールの法則の微分形である。
rotは回転成分を抽出する微分演算であり、ローテーションと読む
(物理数学「ローテーション(回転)」参照)。
この式の意味はアンペールの法則の積分形と同じで、電流が
回転する磁場を生むということである。
積分形では有限の大きさの閉曲線Cを考えたが、
微分形はある一点についての法則である。
アンペールの法則もガウスの法則と同様、実際の磁場を求めるときには
積分形の方が有功である場合が多い。
次節にアンペールの法則で磁場を求める例を用意したので、
アンペールの法則の有効性を感じて欲しい。
|
|

