前節では、定常電流による磁場をアンペールの法則により
求めた。 アンペールの法則は対称性を利用すると
非常に簡単に磁場を求めることができた。
対称性が良くない場合は、アンペールの法則では
磁場を求めることができない。
そこで、この節で導入するビオ・サバールの法則が必要になる。
前節の最後に、線電荷及び線電流は逆1乗則、面電流及び面電荷は
定数の場が生じることに触れた。
これらをまとめてみると、以下のようになっている。
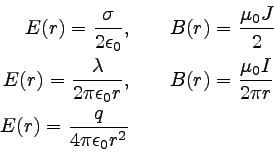 |
… (1) |
上段が面電荷および面電流、中段が線電荷および線電流、下段が点電荷による
場の様子である。
面電荷については扱っていなかったが、
ガウスの法則を使えば簡単に求められる。 σは
面積あたりの電荷分布である。
これらの式の電場と磁場を比較してみると、
非常に良く似た関係があることがわかる。
比例定数のε0とμ0は分母分子逆にあるが、
それ以外の定数、rの次数は一致している。
このことから、もし「点電流」を考えることができれば、
これは逆2乗則になるのではないかと考えられる。
式の類似関係から、「点電流」の密度をiとすると、
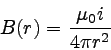 |
… (2) |
という風に想像できる。
これを定式化するとビオ・サバールの法則になる。
ここでは、これを類似関係から類推した。
証明はベクトルポテンシャルを導入するとできるが、
現段階では少し難しくなってしまうので省略することにした
(ベクトルポテンシャルについては記事を作成予定)。
電流は回路内を流れるものであり
「点電流」というものは存在しないので、iを
他のもので表す方法を考えてみよう。
直線電流の場合と比較すると、この式には分母にrが増えている。
よって、iの次元は[電流]×[長さ]であることがわかる。
点電流に相当するものとして、電流を微小な長さで切り出した
「電流素片」というものが考えられる。
電流の微小長さをdsとすると、i=Idsとすれば
「点電流」に対応する式を満たすことがわかる。
ただし、点電荷による電場は放射状に広がったのに対して、
電流素片による磁場は右ネジの方向に発生する。
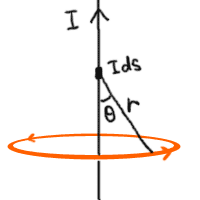
下図のような状況を考えた場合、電流素片から発生する磁場は
電流の方向とr方向との直交成分のみになると考えられる。
 |
… (a) |
図のように
θをとると、i=Ids×sinθとすればよい。
電流を微小な幅で切り出したので、発生する磁場も
微小量になると考えられる。
そこで、磁束密度の大きさBをdBと書くことにしよう。
するとdBは以下のようになると考えられる。
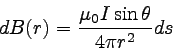 |
… (3) |
磁場はベクトル場なので、大きさだけでなく方向も重要である。
そこで、上の式を方向も含めた形に書き直そう。
電流素片の位置をs、求める磁場の位置をrとすると、
電流素片から磁場に向かうベクトルは(r−s)となる。
また、電流素片の位置sは電流に沿って変化すると考えると、
方向も含めた電流素片を含めたベクトルはIdsとなる。
図示すると以下のとおりである。
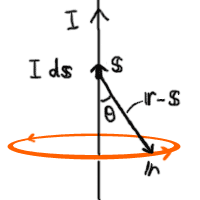 |
… (b) |
電流素片と磁場との距離は|r−s|となる。
磁場の方向は、外積を使って表すとIds×(r−s)
の方向であると言える。
以上のことから、磁束密度の大きさが先ほどの式と同じになるようにすると、
電流素片により発生する微小な磁束密度dBは
以下のように書ける。
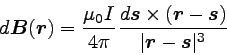 |
… (4) |
外積が出てきたおかげでsinθを式から消すことが出来た
(外積の定義より
|ds×(r−s)|=|ds|×|r−s|
sinθである)。
定常電流からなる回路による磁場は、これを回路に沿って積分すれば
求めることができる。 すなわち、
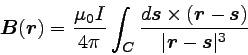 |
… (5) |
となる。 Cは回路に沿った経路である。
これがビオ・サバールの法則である。
この式は実はアンペールの法則と等価であるが、
回路の形がわかっていればアンペールの法則では求めにくい
磁場も求めることができる。
ビオ・サバールの法則は、電流密度ベクトルを使って書き直すことができる。
電流密度は、ある点を通過する電流を表すベクトルであった。
電流は有限の大きさの面を通り抜ける電荷の総量であったので、
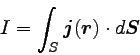 |
… (6) |
という関係があることを前節で扱った。
これをビオ・サバールの法則の式に導入してみよう。
dsの方向は電流の方向なので、電流密度と平行になっている。
そこで、dsをjで代用することにしよう。
ビオ・サバールの法則の式の中には電流Iがあったので、
jを面積分しなければならない。
これと回路に関する積分とあわせて、体積積分するとよいことになる。
電流のある範囲の空間をVとすると、以上のことからビオ・サバールの法則は
以下のように書き換えられる。
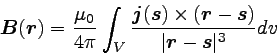 |
… (7) |
電流がない場所ではjはゼロになるので、積分に影響しない。
そこで、この体積積分は全空間に渡って行えばよいことになる。
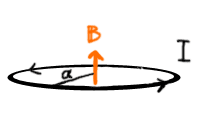
ビオ・サバールの法則を使って、半径aの円電流の中心部に発生する磁場を
求めてみよう。
図で表すと以下のような状況である。
 |
… (c) |
このような電流が作る磁場の場合、アンペールの法則では
求めるのが難しい。 なぜなら、どのような閉曲線Cを考えても
磁場が一定にならず、線積分が求められないからである。
一方、ビオ・サバールの法則を使うと磁束密度は簡単に求められる。
まず、電流を電流素片に分けて考える。 すると、どの電流素片からも
上方向の磁場が発生することがわかる。 よって、電流全体が作る
磁場も上方向をむいていると考えることができる。
磁場の方向がわかったので、大きさを求めよう。
この場合はビオ・サバールの法則の式の絶対値を取って考えればよい。
電流素片の方向とベクトル(r−s)は常に直交するので、
外積の大きさはそれぞれの大きさの積になる。
また、電流素片と円の中心との距離は常に一定なので、
被積分関数は全て定数になる。
残ったdsの積分は、円周の長さに相当するので、2πaとなる。
以上のことをまとめると次のようになる。
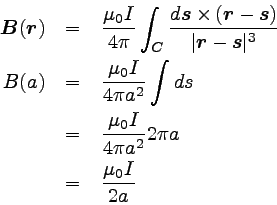 |
… (8) |
半径aに反比例する結果が得られた。 これは、電流が線上を
流れているためだと考えられる。
また、この磁束密度を無限に長い直線電流の場合と比べると、
電流からの距離が同じ場合π倍大きい値であることがわかる。
以上で定常電流に対する定常的な磁場については
終わりである。
定常的な電場及び磁場についてみてきたが、これだけではまだ
マクスウェル方程式の全てが揃わない。
次節からは、時間変化する電場・磁場について扱う。
電磁場の時間変化まで考えたとき、マクスウェル方程式は完成する。
|
|

