今まで静電磁場について扱ってきたが、ここからは
電磁場が時間変化する場合について考えよう。
静電磁場に関して今まで紹介した式のうち特に重要なものは以下の4つである。
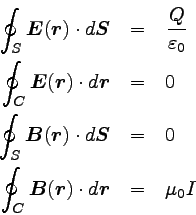 |
… (1) |
一番上はガウスの法則で、電場の源は電荷であることを表す。
2番目は、静電場には回転成分が存在しないことを示す法則である。
3番目は磁場に関するガウスの法則で、磁気モノポールが存在しないことを示す。
最後はアンペールの法則で、電流により渦状に回転する磁場が発生することを
表しているのであった。
電磁気学において非常な重要な式であるマクスウェル方程式は、
以上の式を電場・磁場が時間変化する場合にまで拡張すると得ることができる。
上に書いた式の中の2つは時間変化する電磁場でもそのまま成り立つが、
残りの2つは成り立たない。
この節でそのうち1つを扱い、次節でもう1つを扱う。
まず先に、時間変化する場合もそのまま成り立つ式を紹介しよう。
それは、電場および磁場におけるガウスの法則である。
電磁場が時間変化する場合も、電荷により放射状の電場が発生することは
変わらない。 また、時間変化によって磁気モノポールが発生する
ということもない。
時間変化する電場・磁場は、時間の関数でもあると考えて
E(r,t)、B(r,t)と書くことにする。
tは時間である。 すると、時間変化も考えたガウスの法則は以下のように書ける。
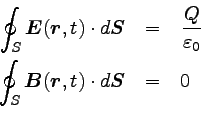 |
… (2) |
この場合の電場に関するガウスの法則の右辺に現れるQは、
時刻tにおいてガウス面Sの内部にある全電荷のことである。
この式は静電磁場の場合と全く同じなので成り立つのはあたりまえだと
思うかもしれないが、これは必然的に成立するわけではない。
ガウスの法則は静電磁場に対する法則から導いたのであって、
時間変化は全く考えられていなかったからである。
ここで時間変化も含めてガウスの法則が成り立つというのは、
静電磁場の場合から類推されたに過ぎない。
しかし、実験事実と比較してみるとどうやら時間変化する場合でも
これらが成り立っているようであることがわかっている。
ここではアンペールの法則の拡張について考える。
定常電流に関するアンペールの法則は、電流密度ベクトルを使うと
以下のように書ける。
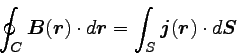 |
… (3) |
ただし、Sは閉曲線Cが囲む任意の面である。
これを変形して、ガウスの法則と同じようにある閉曲面からの電流の
湧き出しがどのようになっているか見てみよう。
そのためには、閉曲面に対する電流密度の面積分を考えればよい。
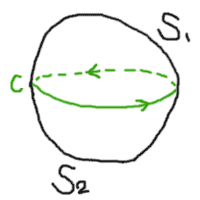
これを求めるために、以下の図に示す閉曲線Cにアンペールの法則を適用する。
 |
… (a) |
まず、下から上に向かってC内を通過する電流について考える。
面Sには、S1を用いることにする。
次に、上から下に向かってC内を通過する電流を考える。
この場合には電流の向きが逆になるので、右ネジの方向を考えて、
Cを図に描いてある矢印の方向と逆向きに積分しなければならない。
同じ経路で逆向きに行う積分は符号が反転する。
アンペールの法則の右辺の面には、S2をとる。
以上のことを数式で書くと、以下のようになる。
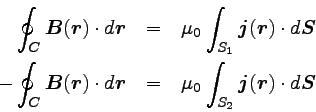 |
… (4) |
この2式の両辺を加えると、左辺は打ち消しゼロになる。
右辺は、S1から出てゆく電流とS2から出てゆく
電流の和になるので、この閉曲面から出てゆく電流の総量になる。
計算して定数μ0で割ると、
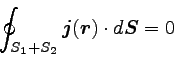 |
… (5) |
という式が導かれる。
これは、電流が湧き出すような原因がないことを示している。
定常電流の場合は、確かにこの式が満たされている。
時間変化しない電流はどこかで発生・消滅せずに、
必ず回路内をループしているはずである。
よっていかなる閉曲面を考えても、その中に入ってくる電流と
出てゆく電流の量は等しくなると考えられる。
しかし、時間変化まで考えた場合はこの結果はおかしいと言える。
なぜなら、この結果だけ見ると新たに電流を発生させたり、
電流を消滅させたりすることが不可能になってしまうからである。
一般の場合には、電場がない状態の導体に電場をかけると
電流が発生する。 このとき、電流は閉曲面から湧き出している。
電流密度の面積分は時間変化を考えたときゼロにはならない。
それでは他の量でどのように表すことができるだろうか?
電流が閉曲面から出てゆくということは、
その閉曲面内の電荷が減ったと言うことができるだろう。
このことから、電流の湧き出し量と電荷の減少量は等しくなると言える。
式で表すと以下のようになる。
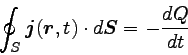 |
… (6) |
ただしQは閉曲面S内の全電荷である。
この式は、電荷は何もない空間から発生・消滅せずに、
電流として拡散してゆくことを示している。
つまり、電荷の総量は変化しないということである。
これは電荷保存則と呼ばれる重要な法則である。
他の法則の時と同じように、電荷保存則にも微分形が考えられる。
特に電荷保存則はガウスの法則と同じ形をしているので、
全く同じようにして微分形を求めることができる。
式だけ書くと以下のとおりである。
わからなくなった場合は「
ガウスの法則」を参照して欲しい。
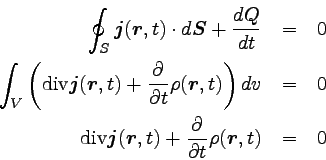 |
… (7) |
この式の途中で微分と積分の交換が行われている。
微分と積分は交換してはいけない場合もあるが、
物理で扱う範囲では問題ない場合が多いので、あまり気にしないことにする。
また、電荷を電荷密度に変えるときにtでの全微分が偏微分になっている。
QはS内の電荷の総量を表すので、tのみの関数であると考えられる。
しかし、電荷密度ρは場所と時間の両方に依存する。
そこで、時間変化だけを考える場合は偏微分にする必要がある。
この電荷保存則(微分系)の形は一般に連続の式と呼ばれていて、
保存則を表す式である。
ここでは電荷についての保存則であるが、流体力学では質量保存則に対応する
連続の式が出てくる。
電荷保存則は重要な法則であるが、
ここで考えていたのはアンペールの法則の拡張についてである。
アンペールの法則をそのまま適用しようとすると、
電荷保存則を満たさなくなってしまう。
そこで、電荷保存則を満たすようにアンペールの法則を
書き換える必要がある。
電荷保存則には、閉曲面S内の電荷の項が現れている。
そこで、ガウスの法則を電荷保存則に適用する。
すると、以下のように両方の項を面積分で表すことができる。
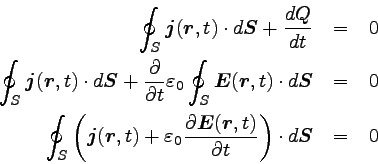 |
… (8) |
この式でも先ほどと同じように微分が途中で偏微分に変わっている。
これは、電場はベクトル場であるために時間だけでなく位置の関数でもあるからである。
また、微分と積分の順序の変更も行った(先ほど書いたように特に気にしないで行ってしまう)。
この式はもちろん時間変化する電磁場に関しても成立する。
閉曲面における電流密度の面積分は、定常電流の場合にはゼロになった。
時間変化まで考えると、今度は(j+ε0∂E/∂t)という
要素の閉曲面における面積分がゼロになった。
そこで、時間変化まで考慮に入れた場合、
電流をε0∂E/∂tの項まで含めて定義すると
良いのではないかと類推できる。
すなわち、
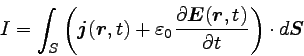 |
… (9) |
である。 電場の時間変化が電流と同じように振舞うと考えるのである。
実際、電場を時間変化させると電流が流れるのに相当する現象が
起こることが確認されている(交流回路におけるコンデンサーなど)。
この新たに加えた電場の時間変化による電流は、
変位電流(変位電流密度)と呼ばれる。
変位電流まで含めた電流を使ってアンペールの法則を書き直すと、
電荷保存則に従う新しい式が得られる。
すなわち、
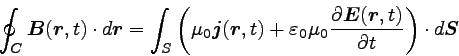 |
… (10) |
である。
これはアンペールの法則の拡張であり、アンペール・マクスウェルの法則と
呼ばれている。
この式は電磁場が時間変化する場合も成り立っている基本方程式である。
電場が時間変化しない場合は電場の時間微分がゼロになり、
アンペールの法則に帰着する。
アンペールの法則のときと同じように、アンペール・マクスウェルの法則に対しても
微分形を求めておこう。 左辺にストークスの定理を適用し、
右辺と同じ面積分の形に変形する。
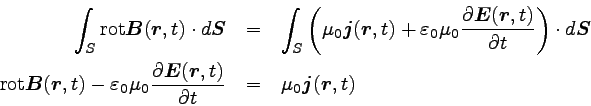 |
… (11) |
ただし、式の2行目で電場の項を左辺に移項した。
電磁場に関する式では、電場・磁場に関する式は左辺に、それらの原因となる電荷・電流は右辺に書く
習慣があるので、ここでもそれに倣った。
以上より、電荷保存則を満たすという要請からアンペール・マクスウェルの方程式を
導いた。
これで、このページの一番はじめに示した4つの方程式のうち3つについて
時間変化する場合に拡張した。
次節では、残りのもう1つの式について時間変化を考えたときどのようになるか考える。
|
|

