前節まででマクスウェル方程式(真空中)を全て紹介した。
この節では、マクスウェル方程式の解に
電磁波に相当するものがあることを紹介する。
ただし、ここではあまり厳密な扱いはせずに、
等速で電磁場が伝わっていく解が存在することを示す。
電磁波の性質については、将来的に記事を作成したいと思っている
(大分先になりそうですが…)。
この節では、電磁場についていろいろな制限をつけて
その解について考えてゆく。
これらは電磁場が一般的に満たす性質というわけではなく、
そういう性質であると仮定しているだけである。
マクスウェル方程式を満たす電磁場は多くの種類のものがあるが、
ここで制限をつけたような解もあるということを紹介するのがこの節の
目的である。
マクスウェル方程式は以下のように書けるのであった。
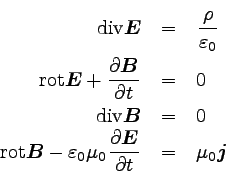 |
… (1) |
この節以降は、電場・磁場は常に時間変化しうると考えて、
関数の引数(r,t)を省略することにする。
まず、電荷も電流も存在しない真空中を考える。
このような状況では、電荷密度と電流密度がそれぞれゼロになる。
するとマクスウェル方程式は以下のようになる。
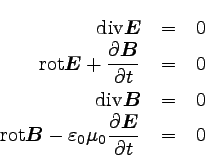 |
… (2) |
次に、電場はx成分のみを持ち、y、z成分はゼロであるとして、
E=(E,0,0)と表すことにする。
また、電場のx成分は時間tとzのみの関数であるとする。
電場はx方向を向いていて、z座標によって大きさが変わる場合を
考えるのである。 磁場もzとtのみの関数で、x、yによらない場合を考える。
これらの場合、電場や磁場をxやyで偏微分するとゼロになる。
これらのことをふまえて、マクスウェル方程式の第2式を計算してみよう。
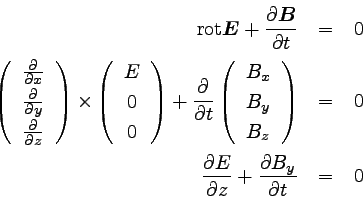 |
… (3) |
2行目を見てみると、第1項についてはy成分のみが残り、
x、z成分はゼロになることがわかる。
そこでy成分のみの関係を取り出して3行目に書いた。
x、z成分は第1項がゼロであったことから、第2項のx、z成分も
ゼロであることがわかる。 すなわち、∂Bx/∂t、∂Bz/∂tは
ゼロになる。
よって、Bx、Bzは時間によらない定数であることがわかる。
今考えているのは時間変化する電磁場であって、時間によらない定数は
無視することにする(電磁波には関係ないから)。 よって、Bx=Bz=0とする。
よって、磁場はy成分のみをもつことになる。
そこで、改めて磁束密度をB=(0,B,0)とおく。
上の式の3行目は後で使うので、☆とおくことにする。
次に、マクスウェル方程式の第4式を計算してみよう。
前節で紹介したとおり、ε0μ0は1/c2と
書ける。 これを使い、実際に計算を行う。
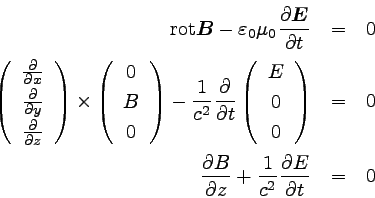 |
… (4) |
2行目を計算すると、x成分以外はゼロになる。 x成分を取り出すと
3行目になる。 この3行目は※とおく。
☆と※を連立して、Eだけの式とBだけの式を作ろう。
まず※をtで偏微分する。 偏微分の順序は交換可能であることから、
∂B/∂tを☆を使って書き直す。 すると、Eのみの偏微分方程式が得られる。
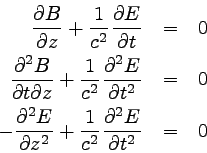 |
… (5) |
次に、☆をtで偏微分する。
偏微分の順序は交換可能なので、∂E/∂tを※を使って
書き直す。 結果、今度はBのみの式になる。
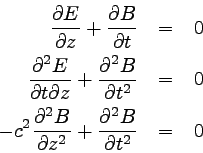 |
… (6) |
EとBの偏微分方程式を比較してみると、
全く同じ形の方程式になっていることがわかる。
すなわち、以下のような形の方程式である。
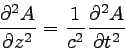 |
… (7) |
これは(1次元の)波動方程式と呼ばれる方程式である。
この方程式の解は、f(z−ct)またはf(z+ct)という形の解を
持つことが知られている。
確認のため、これらの解を波動方程式に代入してみると、
両辺ともf’’という形になり、確かに解になっていることがわかる。
このf(z−ct)やf(z+ct)という解がどういう性質を持つか
考えてみよう。
まず、t=0ではこれらの関数はf(z)という形を持つ。
そして時間がたつとt>0となる。 このとき、f(z−ct)
はf(z)をz方向にctだけ平行移動したものになっている。
一方、f(z+ct)は−z方向にctだけ平行移動したものになる。
移動距離は時刻が経つほど大きくなるので、
これはz方向および−z方向に伝わる波であると考えられる。
図で表すと以下のようになっている。
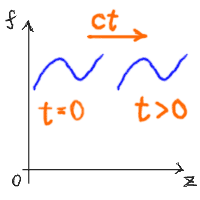 |
… (a) |
時刻がt進むごとにctだけ進行する波なので、
その速度はcであることになる。
電場のx成分と磁場のy成分がこの形の式になったので、
電場と磁場は速さcで伝わる波であるということになる。
これが電磁波である。
cは電磁波の速度、すなわち光速度であることがわかる。
電磁波の性質について少し紹介しよう。
ここでは色々な制限をつけてマクスウェル方程式を
解いていったので、電磁波がここでの解のような性質を
持つとは限らない。 しかし、いくつかの性質は
電磁波の一般的な性質である。
まず、電磁波中の電場と磁場は直交している。
ここでは電場がx方向を向いていると仮定して、
磁場がy方向を向いていることを導くことが出来た。
次に、電場・磁場の方向と進行方向が直交しているという性質がある。
この場合は電磁場はx方向とy方向であるのに対し、進行方向はz方向であった。
この性質は、「電磁波は横波である」という風に表現される性質である。
進行方向に対し変位が横向きなのでこのように表現される。
以上で真空中の電磁気学は終わりである。
しかし、まだ説明していない事項もいくつかあるし、
物質中の電磁気学に関しては全く説明していない。
これらについては、いつか記事を作成したいと思っている。
気長にお待ちいただければ幸いである。
|
|

