真空中に電荷があるとき、発生する電場はクーロンの法則に従う。
しかし、真空中に電荷の他に導体がある場合は電気力線が等方的に
発生しなくなる。
ここでは、そのような場合に電場を用いる方法の一つについて扱う。
電荷により発生する静電場の求め方について、
ガウスの法則を使った方法を紹介した。
ガウスの法則は非常に有効だが、電荷のまわりに対称性がない場合は
適当なガウス面を選ぶことが出来なくなり、電場を求めるのは難しくなる。
そのような場合は、静電ポテンシャルを求めるとよい。
静電ポテンシャルをφとすると、電場Eは
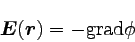 |
… (1) |
という風に表すことが出来るのであった。
よって、静電場を求める場合には静電ポテンシャルがわかればよいことになる。
電場はベクトル場で3成分あるのに対し、静電ポテンシャルは
スカラー場なので1成分のみである。
「静電ポテンシャルとコンデンサー」で
紹介した通り、点電荷による静電ポテンシャルは
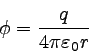 |
… (2) |
という風に書くことができる。
ただしrは電荷からの距離で、qは電荷である。
静電ポテンシャルは基準をどこにとるかによって定数分だけ自由度があるが、
ここでは電荷の影響を全く受けない場所である無限遠方でゼロになるように
している。
(2)式は真空中の場合の式であって、近くに導体があると成り立たない。
導体とは金属のような電気を通す物質であるということはすでに説明した。
導体中には自由に動ける電子があり、電子は導体内の電場を打ち消すように動く。
そのせいで導体中では電場が存在しないことになる。
電場が存在しないということは、導体中の静電ポテンシャルは一定であるということになる。
静電ポテンシャルが導体の内外で連続であるためには、導体の境界面で
電場が一定でなければならなくなる。
(2)式のみではそのような条件は満たさないので、条件を満たすような
電場を考える必要がある。
このような状況で電場を求める問題を「静電場の境界値問題」と言う。
境界値問題を考えるとき、まず考える必要があるのが
静電場の基本法則である。
div E=ρ/ε0とrot E=0は
常に満たしていなければならない。
静電ポテンシャルで考える場合rot E=0は自動的に
満たされることになる(rot grad φ=0)ので、
ガウスの法則を満たすように考えればよいことになる。
次に考えるべきことは境界条件である。
導体がある場合には、導体表面で静電ポテンシャルが一定になるように
しなければならない。
境界値問題の解法の一つとして、鏡像法と呼ばれるものがある。
鏡像法について考えるために、ここでは一つの具体的な問題を考える。
真空中において、x<0の領域全てが導体で埋まっているとする。
そのとき、x軸上のx=dの点に電荷qがあるとすると、発生する電場はどのように
なるだろうか?
まずガウスの法則から、電荷からある量の電気力線が発生する。
導体表面では電位が一定になるので、電気力線は導体面に
垂直になることがわかる(等ポテンシャル面と電場E=grad φは直交する。
物理数学「grad(勾配)」参照)。
このことから、電気力線を図示すると以下のようになる。
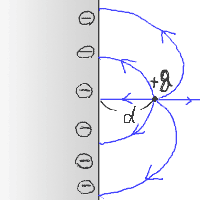 |
… (a) |
図の左側が金属である。 右側にプラスの電荷があるため、
マイナス電荷が金属表面に集まってくる。
そのせいで電気力線が図のようになるのである。
導体は左側無限遠方まで続いているので、
その場所での導体の静電ポテンシャルはゼロになる。
導体中は静電ポテンシャルが一定なので、境界値においても
静電ポテンシャルはゼロでなければならない。
よって、境界条件はx=0においてφ=0ということになる。
この場合、点電荷からなる静電ポテンシャルの式(2)を使って
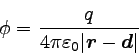 |
… (3) |
(dは電荷の位置)としても境界条件を満たさず、
図(a)のような電場にならないことがわかる。
そこで、境界条件を満たす例として、以下のような状況を考える。
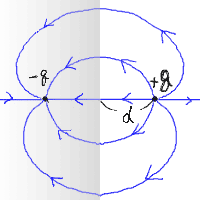 |
… (b) |
境界面の反対側に同じ大きさで符号の違う電荷があると考えるのである。
すると、静電ポテンシャルは
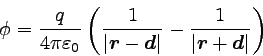 |
… (4) |
となる。
今度は境界条件を満たしていることがわかる。
この静電ポテンシャルは、図の右半分でガウスの法則を満たし、
かつ境界条件を満たす解になっている。
よって、この静電ポテンシャル(4)が実現している静電ポテンシャルで
あることになる。
このように、導体中に仮想的な電荷があると考えると静電場の境界値問題が
解ける場合がある。
これは導体に電荷が鏡のように映っていると考えている
ことになるので、鏡像法(電気映像法)と呼ばれる。
ここで想定される電荷は鏡像電荷(電気映像)と呼ばれている。
もちろん実際に導体中に電荷−qがあるわけではない。
実際に発生する電荷分布は、図(a)のような
金属表面の連続的な分布である。
しかし、どちらの場合も金属の外で発生する電場は
同じである。
なぜなら、静電場の基本法則を満たし、かつ境界条件を満たす電場は
ただ一通りしかないからである。
図(b)には左半分にも電気力線を描いたが、
実際には導体中には電場は発生しないことに注意すべきだ。
静電ポテンシャルは常にゼロであり、その勾配も
常にゼロベクトルである。
鏡像法の例をもう一つ見てみよう。
半径aの導体球の近くにプラスの電荷qがあるとする。
電荷の位置は導体球の中心から距離dの位置にあるとする
(ただし電荷は球の外にある、つまりd>aとする)。
この場合は、導体球がどのような状態になっているかによって
電場の様子が変化する。
まず、導体球が銅線などで地面に接続されている場合を考える。
このように地面に接続することを「接地する(アースする)」と言う。
導体が接地されている場合、その導体の静電ポテンシャルはゼロになる。
なぜなら、地面は非常に大きな導体なので、上で扱った無限の大きさを持つ
導体と同じように働くからである。
実際には地球は有限な大きさを持っている。 しかし、
普通の静電気的現象に比べればはるかに大きい。
よって、地球全体がある特定の静電気的な影響を受けることはないと
考え、電位はゼロであるとするのである。
接地されている導体の場合、地面と電子のやりとりを自由にすることができるので、
プラスまたはマイナスに帯電することができる。
今考えている状況では、導体球の近くにプラスの電荷があるので、
導体はマイナスに帯電すると考えられる。
このこととガウスの法則、及び境界面と電場が直交することを
考慮すると、電気力線は以下のようになる。
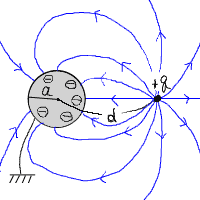 |
… (c) |
球の左下に描いてある線は接地されていることを表している。
このような境界条件を満たす鏡像電荷はどのようなものか考えてみよう。
まず、球はマイナスに帯電することがわかるので、
鏡像電荷の符号はマイナスであることがわかる。
そこで、その電気量を−q’とおくことにする。
次に、鏡像電荷は球の中心と電荷qの結ぶ直線の上にあり、
球の中心よりは電荷qに近いところにあると考えられる。
球の中心と鏡像電荷の距離をbとする。
これらのことをまとめて図示すると、以下の通りになる。
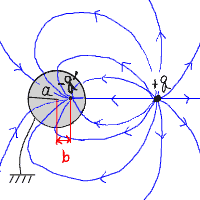 |
… (d) |
導体内にも電気力線を描いたが、実際には電気力線は存在しない。
この電気力線は、鏡像電荷があって導体が存在しないときのものである。
次に、境界条件を満たすようにq’とbを決める必要がある。
導体が接地されているため、境界条件は球上で静電ポテンシャルが
ゼロであるということである。
そこで、球の図における右端と左端の静電ポテンシャルを
(2)式によって具体的に計算すると、以下のような連立方程式が得られる。
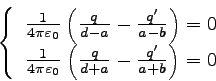 |
… (5) |
これを解くと、結果は
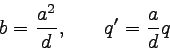 |
… (6) |
となる。
ここでは右端と左端における境界条件のみを考えたが、
球の上のほかの点についても静電ポテンシャルは(6)式の
条件でゼロになることが確かめられる。
鏡像電荷の位置と電気量がわかったので、
電荷qと鏡像電荷のポテンシャルを計算し足し合わせれば
導体外の空間の静電ポテンシャルを求めることができる。
次に、同じ状況で導体が接地されていない場合を考える。
他の導体に接続されていない場合、その導体は「絶縁されている」と言う。
ここでは絶縁されている導体球を考える。
接地されている場合と違い、今度は導体の静電ポテンシャルはゼロになる
必要はない。
ただし、導体中で一定でなくてはならない。
また、絶縁されている導体は全体としてプラスまたはマイナスに帯電することは
できない。
電子が移動してマイナスの個所が発生しても、
変わりに別の場所がプラスになるのである。
導体の電荷は全体で正味ゼロである。 よって、
ガウスの法則より導体に入ってくる電気力線と導体から
出てゆく電気力線の量は同じでなければならないことになる。
このことと境界条件を考えて電気力線の様子を描くと、以下のようになる。
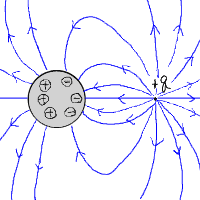 |
… (e) |
導体の右側にプラスの電荷があるので、電子が右側に集まっている。
一方、電子を失った左側はプラスになっている。
プラスに帯電した左側からは電気力線が発生し、そのせいで
導体から出入りする電気力線の量は等しくなる。
この場合も鏡像電荷を考えよう。
今回は導体中の電気量の合計がゼロになるので、
複数の鏡像電荷が必要になる。
まず一つ目は、接地した場合の鏡像電荷−q’を
先ほどと同じ場所に置く。
すると、導体表面で静電ポテンシャルはゼロになる。
この状況で球の中心にプラスの電荷q’を置くと、
全体で電気量がゼロになる。 さらに、
球の中心の電荷による電位は球の表面で一定なので、
境界条件も満たされることになる。
導体の静電ポテンシャルは境界値と同じ一定の値なので、
先ほどと違いゼロではなくプラスの値を持つことがわかる。
鏡像電荷の様子を図示すると、以下の通りである。
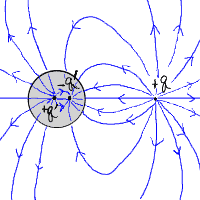 |
… (f) |
もちろん導体球の中では電場は生じない。
この図の電気力線は、導体が存在せず鏡像電荷が実際に存在するときの
電場の様子である。
電荷と導体が同時にある場合は、以上のように鏡像法により
電場を求めることができる場合がある。
境界値問題に対してこの方法はいつでも使えるのではなく、
境界条件を満たすような鏡像電荷を想定できる場合のみである。
境界値問題の他の解法としては、ラプラス方程式の
極座標における一般解を使う方法がある。
|
|

