丂暔棟偱偼懡偔偺暔棟検傪埖偆偑丄偦傟傜偺拞偵偼
偳偪傜偺曽岦傪岦偄偰偄傞偐偑廳梫側堄枴傪帩偮傕偺偑偁傞丅丂
椺偊偽丄懍搙丄椡側偳偑偁傞丅丂
懍搙偺応崌丄偳偺偔傜偄偺懍偝乮俀侽侽倠倣乛倛側偳乯偱摦偄偰偄傞偐傕
廳梫偩偑丄偳偪傜偺曽岦偵乮怴戝嶃偵岦偐偭偰丄側偳乯摦偄偰偄傞偐傕峫偊傞傋偒偩傠偆丅丂
偙傟傜偼儀僋僩儖傪巊偭偰昞偡偙偲偑偱偒傞丅丂
堦曽丄岦偒傪峫偊傞昁梫偑側偄傕偺傕懡偔偁傞丅丂
椺偊偽丄壏搙丄帪娫丄柺愊側偳偱偁傞丅丂
壏搙偼壗搙偱偁傞偐偩偗偑栤戣偵側傞偺偱偁偭偰丄
乽惣岦偒偵俀侽亷乿側偳偲尵偭偰傕堄枴偑側偄丅丂
偙傟傜偺丄儀僋僩儖傪巊傢側偄偱悢偺傒偱昞偡検偺偙偲傪
僗僇儔乕検偲屇傇丅丂
崅峑傑偱偺暔棟偱偼丄儀僋僩儖検傪栴報偱昞偟偼偡傞偑
儀僋僩儖偺惉暘傪峫偊偰墘嶼傪峴偆偙偲偼側偐偭偨丅丂
儀僋僩儖夝愅偼戝妛埲忋偺暔棟偺戝偒側摿挜偱偁傞丅丂
丂崅峑悢妛偱偼儀僋僩儖偼暥帤偺忋偵栴報傪偮偗偰昞偡偑丄
戝妛悢妛偱偼懢帤傪巊偭偰昞偡偙偲偑懡偄丅丂
怴僀僔僇儚暔棟妛尋媶強偱偼丄偙偺昞婰偵姷傟傞偲偄偆堄枴傕偙傔偰
懢帤偱昞婰偟偰偄傞丅丂
椺偊偽丄俙偲偄偆晽偵昞婰偡傞丅丂
栴報偱昞偡偐懢帤偱昞偡偐偼扨側傞彂偒曽偺堘偄偱偁偭偰丄
杮幙揑側堘偄偼慡偔側偄丅丂
丂庤彂偒偱儀僋僩儖傪懢帤偱昞婰偡傞応崌丄
廲慄傪揔摉偵侾杮懌偟偰昞婰偡傞丅丂
椺偊偽埲壓偺傛偆偵側傞丅丂
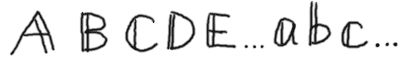 |
丂丂丂乧丂乮倎乯 |
偙偙偵彂偄偨偺偼堦椺偱偁偭偰丄懢帤偱偁傞偲傢偐傟偽
偁傞掱搙帺桼偵昞婰偟偰傛偄丅丂
乽僼傽僀儞儅儞暔棟妛乿揹帴婥妛偺戞俀復偵
庤彂偒懢帤儀僋僩儖偺椺偑慡傾儖僼傽儀僢僩嵹偭偰偄傞偺偱丄
嶲徠偟偰偐偭偙偄偄庤彂偒儀僋僩儖傪捛媮偡傞偲傛偄
乮擔杮岅斉僼傽僀儞儅儞暔棟妛偵傕嵹偭偰偄傞偐偳偆偐偼枹妋擣乯丅丂
丂儀僋僩儖偲偟偰傛偔巊傢傟傞傕偺偵丄乽埵抲儀僋僩儖乿偲偄偆
傕偺偑偁傞丅丂
堏摦偟偰偄傞暔懱偺埵抲傪帵偡応崌側偳偼丄埵抲傪儀僋僩儖偲偟偰埖偭偨傎偆偑
曋棙偱偁傞丅丂
埵抲儀僋僩儖偼捠忢倰偱昞偡丅丂
偁傞暔懱偑嬻娫嵗昗偱倶嵗昗偑倶丄嵗昗偑倷丄倸嵗昗偑倸偺
埵抲偵偄傞応崌丄
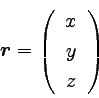 |
丂丂丂乧丂乮侾乯 |
偲偄偆傆偆偵昞偡丅丂
崅峑偱偼庡偵墶彂偒偱昞婰偟偨偲巚偆偑丄
廲彂偒偵偟偨傎偆偑尒傗偡偔丄寁嶼傕偟傗偡偄丅丂
墶岦偒偺昞婰傪墶儀僋僩儖丄廲岦偒傪廲儀僋僩儖偲屇傇丅丂
抧偺暥偱儀僋僩儖傪昞偡応崌偼丄
廲儀僋僩儖偱偼彂偗側偄偺偱墶儀僋僩儖偱倰亖
乮倶丆倷丆倸乯側偳偲昞偡丅丂
丂儀僋僩儖拞偺梫慺偺偙偲傪儀僋僩儖偺惉暘偲屇傇丅丂
幚嵺偵埵抲偑妋掕偟偰偄傞応崌偼儀僋僩儖偺惉暘偼
曄悢偱側偔嬶懱揑側悢偵側傞丅丂
椺偊偽乮侾丆俀丆俁乯偺埵抲傪昞偡応崌丄
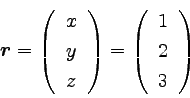 |
丂丂丂乧丂乮俀乯 |
偲彂偗偽傛偄丅丂
儀僋僩儖摨巑偺摍幃偼丄偦傟偧傟偺惉暘偑慡偰摍偟偄偙偲傪昞偡丅
丂巹偨偪偺偄傞嬻娫偼俁師尦側偺偱丄
俁偮偺梫慺傪傕偭偰偄傞儀僋僩儖傪巊偊偽嬻娫忋偺慡曽岦傪
昞偡偙偲偑偱偒傞丅丂
偦偙偱丄暔棟偱巊偆儀僋僩儖検偼懡偔偺応崌俁師尦偺儀僋僩儖傪巊偭偰
昞偡丅丂偨偩偟丄憡懳榑偱偼帪娫傕娷傔係師尦偺儀僋僩儖傪巊偆側偳丄
椺奜傕偄偔偮偐偁傞丅丂
埲壓偱偼丄摿偵抐傜側偄尷傝俁師尦偺儀僋僩儖偱丄惉暘偑幚悢偱偁傞傕偺傪埖偆丅丂
丂儀僋僩儖偺懌偟嶼偲堷偒嶼偼
崅峑悢妛偱廗偆偑丄娙扨偵暅廗偟偰偍偙偆丅丂
儀僋僩儖偺懌偟嶼傗堷偒嶼偼丄惉暘摨巑偵懳偟偰懌偟嶼丄堷偒嶼傪
峴偊偽傛偄丅丂傛偭偰丄寁嶼寢壥傕儀僋僩儖偵側傞丅丂
椺偊偽倰亖乮倶丆y丆倸乯偲倰乫亖乮倶丆倷丆倸乯偺
堷偒嶼偼埲壓偺傛偆偵峴偆丅
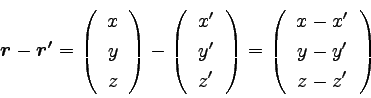 |
丂丂丂乧丂乮俁乯 |
寁嶼偼娙扨偩偑丄偙傟偑恾宍揑偵偳偆偄偆堄枴傪帩偭偰偄傞偐偑廳梫偱偁傞丅丂
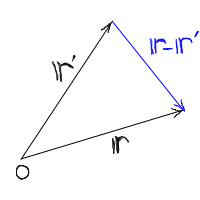
倰亅倰乫偼丄壓恾偺惵偄儀僋僩儖傪昞偟偰偄傞丅丂
 |
丂丂丂乧丂乮倐乯 |
恾傪尒傟偽傢偐傞偲偍傝丄倰亅倰乫偼
倰乫偐傜尒偨偲偒偺倰偺埵抲傪昞偡儀僋僩儖偵側偭偰偄傞丅丂
倰偵偁傞暔懱偲倰乫偵偁傞暔懱偑憡屳嶌梡傪偟偰偄傞応崌偵偼丄
偙偺傛偆側儀僋僩儖偺嵎傪傛偔巊偆丅
丂師偵丄儀僋僩儖偺抣偑曄壔偡傞応崌偵偮偄偰峫偊傛偆丅丂
偙偙偱偼壗偐侾偮偺曄悢偵傛偭偰儀僋僩儖偑曄壔偡傞応崌傪
峫偊傞丅丂
偙偺傛偆側傕偺偱堦斣戙昞揑側偺偼丄
暔棟検偑帪娫曄壔偡傞応崌偱偁傞丅丂
椺偊偽丄埵抲儀僋僩儖偑帪娫曄壔偡傞偲偄偆偺偼丄
暔懱偑摦偔偙偲傪昞偟偰偄傞丅丂
丂帪娫傪寛傔傞偲埵抲偼堦捠傝偵寛傑傞偺偱丄
埵抲偼帪娫偺娭悢偲尵偆偙偲偑偱偒傞丅丂
偙偺傛偆偵丄娭悢偱偁傞儀僋僩儖偺偙偲傪儀僋僩儖娭悢偲尵偆丅丂
椺偊偽丄埵抲儀僋僩儖偑帪娫偺娭悢偱偁傞偙偲傪昞尰偡傞応崌丄
倰乮倲乯偲偄偆傆偆偵彂偔丅丂
儀僋僩儖娭悢偼丄惉暘偑偦傟偧傟撈棫偟偨娭悢偵側偭偰偄傞丅丂
偡側傢偪丄倰乮倲乯亖乮倶乮倲乯丆倷乮倲乯丆倸乮倲乯乯偲偄偆偙偲偱偁傞丅丂
儀僋僩儖娭悢偵懳偟偰丄儀僋僩儖偱側偔僗僇儔乕偺
娭悢偼僗僇儔乕娭悢偲屇偽傟傞丅
丂儀僋僩儖娭悢偵偮偄偰傕旝暘傪峫偊傞偙偲偑偱偒傞丅丂
帪娫曄壔偡傞埵抲儀僋僩儖倰乮倲乯椺偵偲偭偰峫偊偰傒傛偆丅丂
儀僋僩儖娭悢傪旝暘偡傞応崌丄偦傟偧傟偺惉暘傪旝暘偡傟偽傛偄丅丂
偡側傢偪丄埲壓偺傛偆偵偡傞丅丂
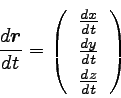 |
丂丂丂乧丂乮係乯 |
懌偟嶼傗堷偒嶼偲摨偠傛偆偵丄寁嶼曽朄帺懱偼扨弮偱偁傞丅丂
偙偺応崌傕傗偼傝旝暘傪偟偨偲偒偵偳偺傛偆側儀僋僩儖偵側傞偐偑
廳梫偱偁傞丅丂偦偙偱丄旝暘偺掕媊偵栠偭偰峫偊偰傒傛偆丅丂
儀僋僩儖娭悢偺旝暘偺掕媊偼僗僇儔乕娭悢偺掕媊偲摨偠傛偆偵丄
埲壓偺傛偆偵側偭偰偄傞丅丂
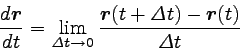 |
丂丂丂乧丂乮俆乯 |
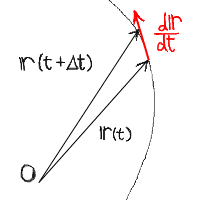
偙傟傪恾帵偟偰峫偊偰傒傛偆丅丂
傑偢丄帪娫曄壔偵傛傞儀僋僩儖倰偺婳摴傪昤偔丅丂
偡傞偲倰乮倲乯偲倰乮倲亄嚈倲乯偼丄偙偺婳摴忋偺揰傪
偦傟偧傟巜偡偙偲偵側傞丅丂
嚈倲偑彫偝偄嬌尷傪庢傞偙偲傪峫偊傞偲丄
倲偐傜倲亄嚈倲傊偺帪娫偺曄壔偼偛偔傢偢偐偩偲偄偆偙偲偵側傞丅丂
偙偺娫偱偺埵抲儀僋僩儖偺曄壔傕傢偢偐偱偁傞偲峫偊傜傟傞丅丂
旝暘偟偰摫偄偨摫娭悢乮偙傟傕儀僋僩儖偱偁傞乯偼丄
埲壓偺愒偄晹暘偺傛偆偵側傞丅丂
 |
丂丂丂乧丂乮們乯 |
嚈倲偑彫偝偄嬌尷傪偲傞偲丄倰乮倲乯偲倰乮倲亄嚈倲乯偼
旕忢偵嬤偔側傞丅丂
偙偺偙偲偐傜丄摫娭悢偼婳摴偵懳偟愙慄偺曽岦傪岦偄偰偄傞儀僋僩儖偵
側傞偙偲偑傢偐傞丅丂
傑偨丄摫娭悢偺戝偒偝偼丄帪娫偵懳偟偰埵抲偺曄壔偑媫寖偱偁傞傎偳
戝偒偔側傞丅丂
偙傟傜偺偙偲偐傜丄埵抲儀僋僩儖傪帪娫偱旝暘偡傞偲
懍搙儀僋僩儖偑摼傜傟傞偲偄偆偙偲偑傢偐傞
乮徻偟偔偼椡妛偺儁乕僕偵彂偔梊掕乯丅丂
丂偙偙偱徯夘偟偨偺偼帪娫曄壔偡傞埵抲儀僋僩儖偺応崌偱偁傞偑丄
懠偺儀僋僩儖娭悢偺応崌傕旝暘偡傞偲婳摴偵懳偟愙慄曽岦傪岦偄偨儀僋僩儖偑摼傜傟傞丅
|
|

