前節ではベクトルの足し算、引き算と微分について紹介した。
ここでは、ベクトル同士の掛け算である内積と外積を紹介する。
ベクトルの足し算・引き算は、成分同士を足し引きすることで
定義された。 計算の結果できたベクトルは、
二つのベクトルの合成を表すのであった。
しかし、成分同士をかけても特に重要な意味を持たない。
そこで、重要な意味を持つ演算である内積と外積が
よく使われる。
まずは内積から。
内積は高校数学でも習うはずなので、知っている人も
多いのではないかと思う。
内積は二つのベクトルからスカラーを作る演算である。
このことから内積は「スカラー積」と呼ばれることもある。
ベクトルaとbの内積は
a・bとドットを使って表現する。
a=(ax,ay,az)、
b=(bx,by,bz)とすると、
これらの内積は以下のようになる。
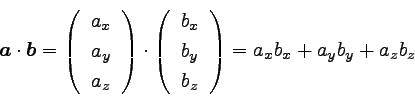 |
… (1) |
それぞれの成分同士を掛け合わせ、それらを足したものが
内積になる。
内積の計算方法はわかりやすいので問題ないと思うが、
以下のように計算している。
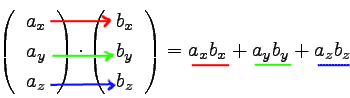 |
… (a) |
赤→緑→青の順に(別にこの順でなくてもよいが)、掛け算をして足し合わせればよい。
ここでは3次元で成分が実数であるベクトル(実ベクトル)を扱っているので
問題ないのだが、成分が複素数の場合は定義のされ方が違うので
注意すべきだ。 複素数を成分に持つベクトル(複素ベクトル)は、
量子力学でよく使われる。
内積の中でも、同じベクトル同士の
内積は非常に重要である。
例えばベクトルa同士の内積は
a2や|a|2と表記される。
これらは、元のベクトルの大きさの自乗を表す。
ベクトルaの大きさは|a|と書く。
これは、以下のようにして求めることができる。
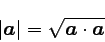 |
… (2) |
内積の計算方法は比較的簡単だが、内積が何を表すのか
考えてみよう。
ベクトルaとbの内積は、
それぞれの大きさを用いると以下のように書ける。
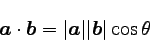 |
… (3) |
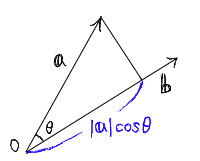
ただし、θはaとbとのなす角である。
これを図で表すと以下のようになる。
 |
… (b) |
このように内積は、1つのベクトルからもう1つのベクトルの方向の成分を
取り出したもの(正射影)に、もう1つのベクトルの大きさを掛けたものである。
それぞれのベクトルの大きさが変わらない場合、内積は
ベクトル同士が平行なときに最大になる。
また、大きさにかかわらず、ベクトル同士が直交している場合は
内積はゼロになる。
次に外積について。 外積はベクトルとベクトルから
ベクトルを作る演算であり、「ベクトル積」とも呼ばれる。
ベクトルaとbの外積は
a×bと表現する。
a×bは計算方法は以下のとおりである。
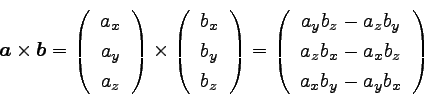 |
… (4) |
注意すべき点は、新しいベクトルのx成分には、
もとのベクトルでx成分だったものが入らないということである。
x成分に入るのはもともとy、z成分にあった要素である。
y、z成分も同様になっている。
これは少し複雑なので、計算方法を解説しよう。
外積を計算するには、まず2つのベクトルの成分を書き、
それらの下にx成分をもう1度書き加える。
そして、以下の矢印のように掛け算を行う。
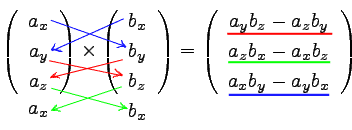 |
… (c) |
まずx成分を計算するには、もとのベクトルのy成分とz成分に注目する。
そして、(左上)×(右下)−(右上)×(左下)を計算する。
以下、同じように赤→緑→青の順に(この順でなくてもよいが)計算する。
外積の計算によってできるのはベクトルであるので、
大きさと向きがそれぞれどうなるかを見ていこう。
まず、大きさは以下のようになる。
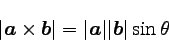 |
… (5) |
θはそれぞれのベクトルのなす角である(この場合θは鋭角にとる)。
これは、ベクトルが作る平行四辺形の面積に等しい。
一方、外積の作るベクトルの方向は、
元のベクトルとはどちらとも直交している。
その方向は、a、b、a×bが
右手系をなすような方向になる。
右手系をなすとは、右手で「フレミングの法則」の形を作ったときに、
親指、人差し指、中指が示す方向の組み合わせになっていることである。
すなわち、外積の方向は以下のようになる。
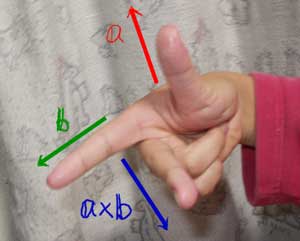 |
… (d) |
ちなみに空間の直交座標ではx軸、y軸、z軸は右手系を
なすように定義する。 3次元の図を書くときに間違えないよう注意しよう。
以上のことをまとめると、外積は以下のように図に描ける。
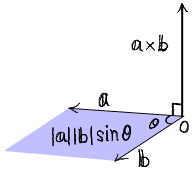 |
… (e) |
外積はグレーになっている部分に対応する大きさをもつことになる。
このような性質から、平行なベクトル同士の外積はゼロベクトルになる。
なぜなら、平行なベクトルが作る平行四辺形の面積はゼロになるからである。
また、外積は掛ける順番によって結果が変わることにも注意しなければならない。
実際に掛ける順番を変えると、a×b=−b×a
となる。 ベクトルの大きさは面積なので変わらず、向きが逆になっている。
これは、外積が右手系をなしていることから説明できる。
親指と人差し指が逆の場所になると、中指の方向は逆方向になる
(指をつらないように注意しながら確かめてみて欲しい)。
|
|

