「ベクトル関数と微分」では
1変数のベクトル関数を扱った。
しかし、物理で扱うベクトルの中には2変数以上の変数による関数も多く存在する。
その中でも特に重要なのが、位置の関数になっているものである。
この世界は3次元なので、位置の関数ということはx、y、zの3つの変数による
関数だということになる。
このような関数の中でスカラー関数のものをスカラー場、
ベクトル関数のものをベクトル場と言う。
これらの関数は、実際に空間の中に分布していると考えられるものが多い。
そこで、場所に遍在しているという意味で「場」という言葉を使う
(通常物理で「場」といった場合4つの力(重力、電磁力、強い力、弱い力)の場
を指すことが多が、ここでは一般的な位置の関数を想定している)。
スカラー場とベクトル場について、具体例をあげながらどういうものだか
考えてみよう。
まずはスカラー場。 ある関数fがスカラー場であるとき、
これは位置座標x、y、zの関数なので、f(x,y,z)と表す。
また、位置ベクトルが決まればfの値が決まることから、f(r)と
表現することも多い。 スカラー場の代表的なものとしては、温度分布が
考えられる。 温度は場所によって変化し、遍在するので「場」を形成していることになる。
他にも、圧力、密度などは大きさをのみを考えればよく(ベクトルでなく)、
空間に遍在しているのでスカラー場を形成している。
一方ベクトル場は、空間に遍在していて、さらにベクトルで
あるもののことである。
あるベクトル関数Aがベクトル場であるとき、スカラー場の時と同じように
A(x,y,z)、A(r)と表記する。
この場合、x、y、zの3つの変数を指定することにより、
ベクトルの3つの成分が決定することになる。
ベクトル場の例としては、風の速度分布が挙げられる。
風は空間上のいろいろな点で観測することができ、全ての点で向きが重要な量である。
風が吹いていないときはその場所の速度ベクトルはゼロベクトルということになる。
天気予報の風の様子は、まさにベクトル場を表している。
天気用法の図のように、ベクトル場は全空間にベクトルがびっしり詰まっている
ようなイメージでとらえるとよいと思う。
場所を決めるとベクトルが決まるのである。
ベクトル場の例は、他に電場、磁場などが挙げられる。
ベクトル場は空間にベクトルが分布していると考えられるが、
それぞれのベクトルはばらばらの方向を向いているわけではなく、
規則正しくならんでいる場合が多い。
このような場合、ベクトルの軌道は滑らかな曲線を描く。
このとき、このベクトル場は何らかの流れを示していることになる。
風の速度分布の場合には空気の流れである。
このように、ベクトル場とは流れの場であると言うことができる。
スカラー場やベクトル場の中には、時間によって変化するものが多い。
例えば、温度分布、風の分布などは時間によって大いに変化するだろう。
このような場合は、スカラー場ならf(r,t)、ベクトル場なら
A(r,t)というふうに表す。 これらは
4変数関数である。
これらの時間微分を考える場合は、
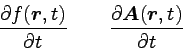 |
… (1) |
というふうに偏微分にしなければならない。
これらの計算を実際に行う場合は、それぞれの成分をtで偏微分すればよい。
スカラー場、ベクトル場に対する微分演算は、
時間に関するもの以外にも重要なものがある。
特に重要なのは、∇(ナブラ)という演算子を
使ったものである。 ∇は以下のように定義されるベクトルである。
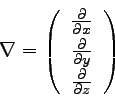 |
… (2) |
ナブラはベクトルなので、作用の仕方にはいくつかのパターンがある。
まず、スカラー場に作用する場合は、スカラー場からベクトル場を作る
ことになる。
このような演算は∇f=grad fと表現する。
gradはgradient(グラディエント)の略で、日本語では勾配と言う。
∇がベクトル場に作用する場合、ベクトル同士なので
内積の形で作用する場合と外積の形で作用する場合がある。
内積の場合、∇・A=div Aと書く。
divはdivergence(ダイバージェンス)の略で、日本語では発散と呼ばれる。
外積により作用する場合、∇×A=rot Aと表記する。
このrotはrotation(ローテーション)を表す。 日本語では
回転と呼んでいる。
grad、div、rotについては次節以降で説明する。
これらの演算を表記するとき、ナブラを使って書いたほうが
実際の計算はしやすいかもしれない。
しかし、新イシカワ物理学研究所では、それぞれが何を表しているかを
イメージしやすくするため、grad、div、rotの表記を主に使用している。
|
|

