前節ではスカラー場とベクトル場を導入した。
また、微分演算子∇を紹介した。
ここでは、スカラー場にナブラを作用させる、
グラディエントという演算について扱う。
まず、∇の定義を復習しよう。
ナブラは以下のように定義されるのだった。
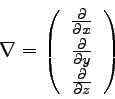 |
… (1) |
あるスカラー場をfとすると、fに∇を作用させることが
できる。
スカラー場にナブラを作用させてできるベクトルをグラディエント
と言い、∇fやgrad fと表す。
具体的には以下のように計算する。
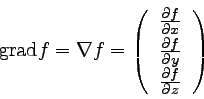 |
… (2) |
スカラー場fは偏微分してもやはり位置の関数なので、
grad fはベクトル場になる。
さて、この新しく出来たベクトル場が何を表すのか考えてみよう。
まずfがxのみの関数で、yやzの関数でない場合について考える。
すると、grad fのy成分とz成分はゼロになる。
x成分は、fの変化が大きい場合には大きくなり、fがあまり変化しない場合には
小さくなる。 また、xが大きくなるにつれfが大きくなる場合は
grad fのx成分は正になり、逆にxが大きくなるにつれfが
小さくなる場合はgrad fのx成分は負になる。
次にfがyによってのみ変化する場合を考えよう。
すると今度は、grad fはy成分のみをもつ。
同じように変化の割合によって、そのy成分の値は変化する。
fがzのみの関数の場合も同様で、grad fは変化の
割合によって変化するz成分を持つ。
以上のことから、grad fは変化の方向に向かうベクトル
であることが推定できる。
grad fが向く向きは、スカラー場fの中で、ある点から
一番増加量が大きくなる方を向く。
また、そのベクトルの大きさはその方向に対する変化の大きさを表す。
温度分布の例で考えてみよう。
部屋の中にストーブがあり、ストーブから離れるほど
温度が低くなるとする。
この状態を表す温度場スカラーをTとすると、grad Tは
温度が一番上昇する方向を向く。 つまり、常にストーブの方向を
向いていることになる。
一方、−grad Tは常にストーブとは逆方向を向く。
これは、ストーブからの熱の流れを表すベクトル場ということになる。
このようにgradは変化量に関するベクトル場を作るので、
日本語では「勾配」と呼ばれる。
2次元のスカラー場を考えた場合、
その値は山のように例えることが出来る。
スカラーの値が大きい場所は高さが高く、小さい場所は低くなると考えるのである。
山の斜面上のある点において、一番勾配が急な部分の、上方向に向かうベクトルが
grad fである。
ただし、実際にはスカラー場は3次元であることに注意する必要がある。
スカラー場の値を山のようにイメージした場合、
等高線に相当するものを考えることが出来る。
すなわち、スカラー場の値が同じ所をつなげたものである。
実際にはスカラー場は3次元なので、値の同じ場所を
つなげていくと面を形成する。
このような面は等ポテンシャル面と呼ばれる。
等ポテンシャル面の方向にはスカラー場の値は全く変化しない。
grad fは最も変化の激しい方向を向くので、等ポテンシャル面
とは直交する。 これは、山の例では等高線と崖の方向が直交する
ことに相当する。
等ポテンシャル面とgrad fが直交する様子は、以下のように図示できる。
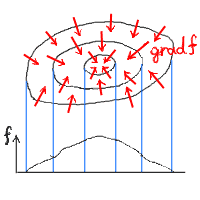 |
… (a) |
図の上側は、ベクトル場grad fの様子と等ポテンシャル面に相当する線である。
下側にあるのはこのスカラー場の様子の断面図である。
これらを比較すると、grad fがfの値が高くなる方向を向く
ベクトル場であることがわかる。
ただし、これらは2次元のスカラー場の表現である。
3次元のスカラー場と等ポテンシャル面の様子を平面上に表現するのは
非常に難しいと思う(私には不可能だ)。
この図から何とか類推していただきたら幸いである。
|
|

