「スカラー場とベクトル場」で
∇演算子を導入したが、∇をベクトル場に作用させる場合には
内積、外積の2通りの方法がある。
ここでは、∇とベクトル場の内積であるdivという演算を扱う。
ナブラの定義は以下のようであった。
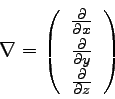 |
… (1) |
あるベクトル場Aに対して、ナブラを内積によって作用させた
結果できるスカラーはダイバージェンスと呼ばれ、div Aと書く。
実際にAのダイバージェンスは、以下のように計算できる。
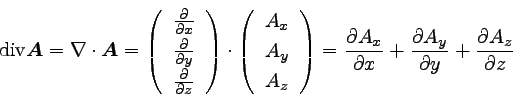 |
… (2) |
内積による演算なので、その結果できるのはもちろんスカラーである。
元のベクトルの各成分が位置の関数だったため、div Aも
位置の関数になる。 よって、このスカラーはスカラー場になっている。
このスカラー場がどのようなことを表しているかを考えてみよう。
まず、∂Ax/∂xについて考える。
これは、ベクトル場のx成分がxで偏微分されているのだが、
そのままでは何を表しているかわかりにくい。
そこで、定義に戻って考えてみよう。
偏微分の定義は以下のとおりである。
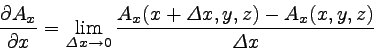 |
… (3) |
ベクトル場Aのx成分についてこのような操作が行われているということは、
図で表すと以下のような様子である。
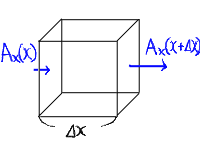 |
… (a) |
この図に描かれている立体は、各辺の長さがx方向は⊿x、y方向は⊿y、
z方向は⊿zであるような直方体である。
まずベクトル場からx成分を取り出すと、青い部分のようにx方向のベクトル
が得られる。
偏微分の操作は、右側のベクトルから左側のベクトルを引き、
その大きさを長さ⊿xで割っていることになる。
これは、この立体からベクトル場のx成分が流れ出た量を表していると
考えられる。
⊿xが小さい極限をとると直方体も小さくなる。
そうすると、∂Ax/∂xはベクトル場のx成分が
ある一点から流れ出した量であると言う事が出来る。
y成分、z成分も同様に、ある点から
流れ出た量を表していると考えられる。 。
div Aはこれらを3成分足したものであるので、
ある一点においてベクトル場が流れ出た総量を表していることがわかる。
このことからこの演算はダイバージェンス(日本語では「発散」)と呼ばれる。
div Aは、ベクトル場Aが各点で
どれだけ発散しているかを与えるスカラー場なのである。
ベクトル場は流れの場であるということに少し触れたが、
ダイバージェンスが正になる点では、流れが湧き出していることになる。
一方、ダイバージェンスが負になる点では流れが吸い込まれていることになる。
風の速度分布の例でいうと、高気圧付近ではダイバージェンスは
正の値を持つだろう。 一方、低気圧の近くではダイバージェンスは負になる。
特に台風の中心などは、ダイバージェンスの絶対値は非常に大きくなるだろう。
ダイバージェンスが正になる典型的なベクトル場は
以下のようなものである。
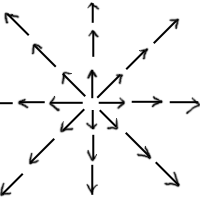 |
… (b) |
中心ではダイバージェンスは間違いなく正の値をとるだろう。
他の点については、ベクトルの大きさの変化のしかたによって
ダイバージェンスの値も変わってくる。
もしベクトル場の大きさが変わらなければ、
まわりに向かって発散していることになるので
ダイバージェンスは正になる。
|
|

