ベクトル場を積分する場合には、
線積分と面積分の2通りの方法がある。
どちらもベクトルを積分して、結果はスカラーになる。
これらはともに物理のいろいろなところで現れる重要な積分である。
まず線積分から。 線積分は、空間上のある経路Cに沿った積分である。
式では以下のように表される。
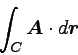 |
… (1) |
drはCに沿った微小なベクトルで、
それぞれの成分は以下のようになっている。
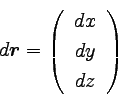 |
… (2) |
線積分ではAとdrの内積を取って積分するので、
ベクトル場の中で経路Cに沿った成分のみを積分していることになる。
ベクトル場は空間中に矢印が分布しているというふうにイメージできるが、
このイメージで考えると線積分は経路Cに沿ってベクトルを
集めていく作業に相当する。
ベクトルをそのまま集めるのでなく、経路C方向の正射影を
集めていくのである。
物理で出てくる例としては、力に逆らって物体を動かすときの
仕事が線積分で表される。
この場合は物体に働く力がベクトル場になっている。
仕事は物体を動かす経路によって変化する。
この積分の値は経路によって大きく変化するが、
積分する方向も重要である。
ベクトル場と同じ方向に向かって積分する場合には
積分の値はプラスになるが、逆向きの場合はマイナスになる。
同じ道のりで方向を変えた場合、積分値の符号が逆になる。
実際に線積分を計算する場合は、まずAとdrを
経路に沿った形に書き直す。
経路は曲線を描くので、1つのパラメータを利用して
表すことが出来るはずである。 このパラメータをtとすると、
Aとdrをtのみを使って表す。
後は内積を使って積分を行えばよい。
例を挙げて線積分を具体的に計算してみよう。
ベクトル場A=(x,−y,0)を以下の経路Cに沿って
線積分する。
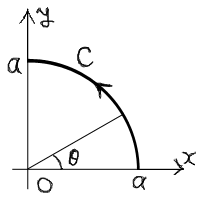 |
… (a) |
経路Cは半径aの円の1/4である。
まず先に内積を計算してみると、以下のようになる。
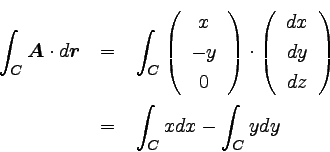 |
… (3) |
ここでそのまま積分してはいけない。
なぜなら、そのまま積分してしまうと経路に関する情報が
入っていないからである。
そこで、パラメータを使って経路を表す。
経路Cは円なので、上の図にあるように角度θをパラメータに選ぶとよいだろう。
θは0からπ/2まで変化することになる。
パラメータを選んだら、Aとdrをθで表す。
x=a cosθ、y=a sinθなので、dx、dyは
以下のように書ける。
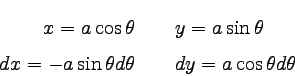 |
… (4) |
これらを代入し、積分をθの積分におきかえる。
そしてθで積分すると、以下のような結果を得る。
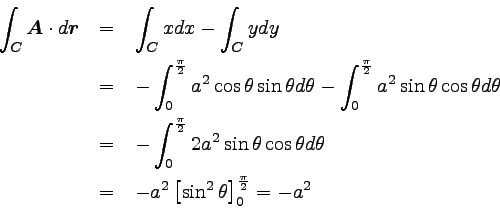 |
… (5) |
次に、面積分である。 面積分は空間上のある面Sに沿った積分である。
式では以下のように表す。
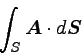 |
… (6) |
dSは面積要素ベクトルというベクトルである。
大きさは微小面積で、方向は面に垂直な方向である。
面積分はベクトル場と面積要素ベクトルの内積をとって積分するので、
ベクトル場の、面積要素ベクトルと平行な成分が取り出されることになる。
面積要素ベクトルと面Sは直交するので、
結局は面積分はベクトル場の、面Sに直交する成分を取り出していることになる。
ベクトル場を、ベクトルが空間中に分布しているイメージで考えると、
面積分は面を通過する矢印を集めることに相当する。
ただし、面を通過するベクトルの、面と直交する成分のみ取り出す。
斜めに面に入射しているベクトルよりも、まっすぐ(垂直に)面に
入ってきているベクトルの方が値は大きくなる。
ここでは面積分は∫A・dSと表記しているが、
∫A・ndSと表現する場合もある。
ndSはdSを方向と大きさに分けて表記した
だけなので、両者は全く同じことを意味している。
また、面積分は最終的に重積分になることのでインテグラルを2つ書いて
表現する場合もある。
このインテグラルの本数も表記の違いであって、本質的には
全く同じことを表している。
物理で出てくる面積分の例としては、磁束密度と磁束の関係がある。
磁束密度は磁場の様子をあらわすベクトル場である。
これをある面で面積分すると、その面を通過した磁束の総量になる。
ベクトル場の説明に風の流れの例を出したが、
この場合には面積分は、ある面を通る空気の総量に対応する。
面積分を実際に計算するには、
まず面Sをパラメータを使って表す。
線積分のときは経路は1つの変数を使って表すことが出来たが、
今度は面なので2変数必要である。
そこで、面を表す変数を2つ用意する。
次に、面積要素ベクトルと積分するベクトル場を
この2つのパラメータを使って表す。
後はこれらの変数について重積分を行えばよい。
面積分も具体例を用いて計算してみよう。
ベクトル場A=(x,y,z)を、
xy平面に平行な面Sについて面積分する場合を考える。
ただし、面Sは常にz=2で、x、yはそれぞれ−1から1までの
値をとる正方形の面である。
この面とベクトル場の様子を図示すると、以下のようになる。
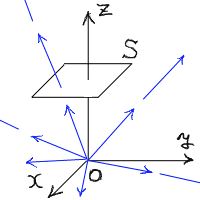 |
… (b) |
青で示したのはベクトル場Aの様子である。
このようなベクトルのうち面を通過するものから、面と直交する成分を集めていく。
これを計算するには、まず面Sを指定するパラメータを探す必要がある。
Sはxy平面に平行なので、パラメータはx、yを指定すればよいだろう。
次に面積要素ベクトルを求める。
面積要素ベクトルの方向は面Sに垂直な向きである。
面に垂直な方向は上方向と下方向の2通りあるが、ここでは
上方向を取ることにする。
どちらの方向を取るかにより積分結果の符号が
変わってしまうので、どちらかは状況に応じて考えなければならない。
上方向を選ぶと、上方向に通過するベクトル場の積分を求めることになる。
面積要素ベクトルは+z方向を向いているということになるので、
z成分のみ持つことがわかる。
その大きさは微小面積である。 この場合、面Sの微小面積は
dxdyで表すことが出来る。 以上から、
面積要素ベクトルはこのようになる。
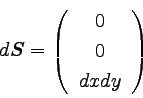 |
… (7) |
面積要素ベクトルが出来たので、今度はベクトル場を
パラメータx、yを用いて書き直す。
ベクトル場の成分は(x,y,z)であるが、
このうちx、yはそのままでよい。 zは他の変数で
書き直さなければならないが、この場合はzは常に一定でその値は2である。
よって、書き直されたベクトル場は(x,y,2)となる。
以上で準備は完了した。 後は内積を取って面積分の値を求めよう。
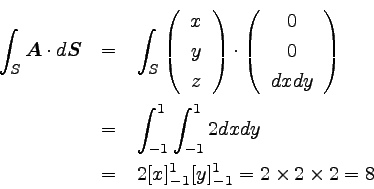 |
… (8) |
xとyは−1から1まで変化するので、以上のような結果が得られる。
線積分と面積分について、意味と計算方法を紹介した。
物理では、実際に計算するよりも意味が重要な場合が多いので、
イメージできるようになることが重要だ。
また、線積分と面積分はガウスの定理、ストークスの定理とともに
出てくる場合が多い。
次節とその次の節でガウスの定理とストークスの定理を扱う。
|
|

