前節では面積分を扱った。
ここでは、面積分に関する重要な定理であるガウスの定理を扱う。
数学的に厳密な証明は行わず、定理の意味を説明する。
まずはじめに、閉曲面に関する面積分を考える。
閉曲面というのは、卵の殻のようなものを想像してもらえればよい。
穴のあいていない曲面で空間を包むのである。
このような面の外側に向かって面積分をする場合、式では
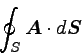 |
… (1) |
と表す。
∫が∮になったが、これは周回積分することを
表している(これは必ず使われる記法ではなく、
そう表現されることもあるだけである)。
さて、このような閉曲面に対する面積分は、
外向きのベクトルを集めることになるので、
内側から湧き出すベクトルの総量を計算していることになる。
湧き出しのない場所では閉曲面に入ってくるベクトルと
出てゆくベクトルの総量が同じになり、積分の値はゼロになる。
一方、入ってくるベクトルの方が多いと
積分の値は負になるが、これは閉曲面内への吸い込みを表す。
湧き出し・吸い込みと言えばdivだが、
divが空間上のある一点に対する演算だったのに対して、
閉曲面の面積分は有限の大きさの空間からの湧き出しを表す。
これらにはこのような違いはあるが、
密接に対応している。
これらの関係を与えるのがガウスの定理である。
ガウスの定理を導くために、面積分を考えた閉曲面内の空間を
小さい直方体に分解して考える。
すなわち、空間を切断していって無数のサイコロ状の空間に分けるのである。
この直方体は、x方向の長さが⊿x、y方向は⊿y、z方向は⊿zとする。
これらの微小な直方体の1つを取ってみると、
ダイバージェンスについて扱ったときと同じ状況になっていることがわかる。
そこで、これらの立体についてダイバージェンスを計算してみる事にする。
divの節で使った図を持ってくると、ダイバージェンスは
以下のような状況をみているのであった。
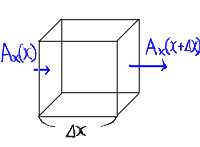 |
… (a) |
x方向に注目すると、右側のベクトルから左側のベクトルを引くことになる。
さて、このような操作を全ての直方体(サイコロ状空間)について
行い、足し合わせることを考えてみよう。
すると、隣り合った直方体では、接している面の部分のベクトルが相殺する。
x方向だけでなくy、z方向にも同様のことを考えると、
直方体同士が接する場合の計算は全て相殺し、
境界面の部分のみの計算に帰着する。
すると境界面でベクトルを集めることになるので、結局閉曲面の面積分に等しくなる。
微小直方体のダイバージェンスをS内の全空間に渡り集める操作は、
∫div Advと書くことが出来る。 ただし、dvは
微小直方体の体積で、dv=dxdydzである。
3変数の積分なのでインテグラルは3つ書くべきであるが、
省略して1つしか書かなかった。
この∫div Advが、接する面同士が相殺して
閉曲面の面積分になるので、
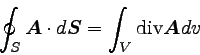 |
… (2) |
が成り立つ。
これをガウスの定理と呼ぶ。
右辺のVは、閉曲面Sで囲まれる全空間を表す。
ガウスの定理の左辺は、閉曲面S全体からの湧き出しを表している。
一方、右辺は微小な湧き出しをS内の全空間について
足し合わせることを表している。
つまり、ガウスの定理とは、微小な湧き出し量を足していくと
全体の湧き出し量になるということを表しているのである。
|
|

