前節ではガウスの定理を扱ったが、これは面積分とダイバージェンスの
対応を与えるものであった。
一方、ストークスの定理は線積分とローテーションの対応を与える定理である。
ここではストークスの定理を、前節と同様に厳密に数学的には取り扱わずに
簡単に説明する。
まず、閉曲線に対する線積分を考える。
閉曲線とは輪っか状に閉じている曲線のことである。
閉曲線の線積分は、閉曲線に沿った成分を取り出して
集めることになるので、ベクトル場が閉曲線に沿っているほど
値が大きくなる。
閉曲線に沿っているベクトル場とは、
その方向に回転している場であると言える。
回転していないベクトル場の場合、経路と同じ方向の
ベクトルと逆方向のベクトルが打ち消しあい、線積分の結果はゼロになる。
閉曲線での線積分は数式では
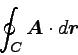 |
… (1) |
と表す。
閉曲面での面積分と同じように∫が∮になった。
今回もやはり周回積分であるので、この記法を用いた。
回転を表す微分演算はローテーションであった。
閉曲線における線積分もベクトル場の回転を取り出すので、
これらは非常に重要な関係がある。
この関係を表すのがストークスの定理である。
ガウスの定理の法則では閉曲面で囲まれた体積を
直方体に切り分けたが、今回は
閉曲線で囲まれた曲面を微小な長方形に切り分ける。
長方形のそれぞれの辺の長さはdx、dyとする。
ここで、ローテーションを導入したときと同じ状況になっていることがわかる。
rotの節から図を引用すると、以下のようなものであった。
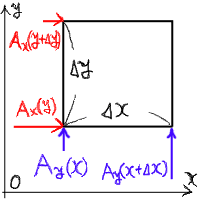 |
… (a) |
青いベクトルは右から左を引き、赤いベクトルは下から上を引くのであった。
この図を意識して、長方形それぞれに対してrotの成分を計算して
足し合わせていってみよう。
すると、
隣接する長方形に対して、接している辺に対応するベクトルが
打ち消しあうことがわかる。
x方向、y方向ともに隣接する辺は相殺するので、
結局周りの辺の要素だけが残る。
すなわち、閉曲線の周りのベクトルを集めることになるので、
閉曲面の線積分に帰着する。
微小長方形に対応するローテーションの成分をを足し合わせたものは、
∫rot A・dSという風に面積分で表すことが出来る。
rot Aはベクトル場であり、面に関する回転成分は
微小面積ベクトルとの内積を取ることにより求められるのである。
積分範囲は閉曲線で囲まれる面内である。
微小な長方形が接している場合は要素が相殺するので、
この面積分が閉曲線の線積分と等しいことになる。
すなわち、
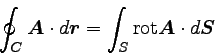 |
… (2) |
となる。
これをストークスの定理と呼ぶ。 Sは閉曲線Cで囲まれる面である。
ストークスの定理の右辺は、微小な回転要素の足し合わせを表している。
一方、左辺は有限の大きさの閉曲線における回転要素である。
つまり、ストークスの定理は、微小な回転要素を集めると
全体の回転になるということを表している式なのである。
ストークスの定理は物理で非常によく使われる。
実際に計算できるようになることも重要だが、
まずはイメージをつかむことが重要である。
|
|

