量子力学は、20世紀前半に成立した新しい分野である。
量子力学と相対性理論の発展により、
それまでの力学と電磁気学は「古典力学」、「古典電磁気学」と
呼ばれるようになった。
量子力学が生まれた背景には、古典力学と古典電磁気学では
説明できない現象が存在するという問題があった。
この節では、まずそれらの問題のいくつかと、
それらから想定される光の粒子性、物質の波動性について紹介する。
ニュートン以来、光とは何であるかというのは大きな問題であった。
ニュートンの考えを受け継ぐ学者たちは、光はプリズムにより7色に分解できるので
粒子であると考えた。
一方、光は水面を伝わる波と同じような波動現象であると
いう考え方もある。
光の正体は長い間謎であったが、古典電磁気学により、
光は電磁波という波動の一種であることがわかった。
これについては
電磁気学の「電磁波」の節で
説明している。
光が電磁波であることがわかって間もない頃、
プランクは高温の物体が光を発すること(高温に熱した物体は
まず赤く光るようになり、さらに高温では白く光るようになる)
についての研究をしていた。
光の発生に対して理想化された物体を黒体と呼ぶが、
黒体の発する電磁波(黒体放射)を説明するには、
電磁波のエネルギーは以下のようなエネルギーの整数倍にしかならない
考えると非常に都合が良いことが発見された。
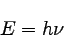 |
… (1) |
Eは電磁波のエネルギーで、
ν(ニュー)は光の振動数である。
hは「プランク定数」と呼ばれる定数で、6.626×10−34[J・s]
という値を持つ。
電磁波のエネルギーは、2hνや5hνという値をとることが
あっても3.7hνや0.4hνという値をとらないと
いうのである。
ただし、hは非常に小さいのでエネルギーはほとんど連続であるかのように
振舞っている。
このエネルギーの最小単位hνは「量子(エネルギー量子)」と呼ばれ、
このように電磁波のエネルギーが離散的な値(不連続な飛び飛びの値)しかとらない
という説は、「エネルギー量子仮説」と呼ばれている。
エネルギー量子仮説は、
不思議ではあるが一見それほど重要でないように思われるかもしれない。
しかし、以下に説明する経緯により、このことが非常に重要な意味をもつことがわかる。
なお、上の式は次のように書かれる場合の方が多い。
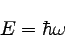 |
… (2) |
ωは電磁波の(角)振動数(1秒間に位相が何ラジアン変化するか)で、
振動数νに2πを掛けたものである。
これら波動に関することがらは、「振動・波動」のページを作って
説明したいと思っている。
ħはプランク定数を2πで割ったもので、エイチバーと読む。
結局hνとħωは全く同じ値をとることになる。
実際に量子力学の計算をする場合はhよりħを使うことが多い。
光の奇妙な振る舞いには、他に「光電効果」と呼ばれる現象がある。
これは、金属に光を当てるとその金属の表面から電子が飛び出すという
現象である。
この現象について、同じ金属に何種類かの強さの光を
当てることを考えていただきたい。
ただし、使用する光は振動数が全て同じ
単色光であるとする。
このとき、強い光を当てたほうが飛び出す電子のエネルギーが
大きくなる(電子のスピードが速くなる)ということが想像される。
しかし、実際には光の強さと電子のエネルギーには関係がないことがわかった。
光の強さを変えても電子のエネルギーは一定で、
飛び出す電子の数が変化した。
すなわち、強い光を当てると弱い光のときよりも多くの電子が飛び出したのである。
一方、同じ強さで光の振動数を変えると、今度は
電子のエネルギーが変化した。
これらは光を単純に波だと考えると上手く説明できない現象である。
この問題に対して、アインシュタインは光を粒子であるとする
驚くべき仮説でこの現象の説明を試みた。
粒子としての光は「光量子(こうりょうし)」と呼ばれ、
アインシュタインによる光の粒子説は「光量子仮説」と呼ばれている。
光量子を1つあたりħωのエネルギーを持った粒子だと考えると、
光の強さは光量子の量に相当し、光の振動数は光量子のエネルギーに
相当すると考えることが出来る。
すると、光電効果が上手く説明できるようになる。
すなわち、強い光を当てると多くの光量子が当たっていることになるため
多くの電子が飛び出す。 光量子1つ当たりのエネルギーは
光の強さによらないので、飛び出すスピードは変わらない。
一方、光の振動数を変えると、光量子1つ当たりのエネルギーが変化するため
飛び出す電子のエネルギーが変化するのである。
光量子は今日では「光子(こうし)」と呼ばれるようになった。
光を粒子と考えると説明できる現象に、コンプトン散乱というものがある。
これは、光が粒子に衝突して粒子の運動量を変えるという現象である。
光は粒子に衝突すると、振動数が変化する。
これも光を波だと考えると説明が難しい現象である。
しかし、光が粒子であり、運動量を持っていると考えると
コンプトン散乱は運動量保存則からきれいに説明できるようになるのである。
粒子としての光の(すなわち光子の)運動量は以下のように表される。
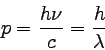 |
… (3) |
cは光速度で、λは光の波長である。
右辺は波動の基本的な式ν=cλを使って書き直した。
このように、運動量も振動数によって変化する値を持つので、
粒子との衝突による運動量の変化で振動数が変化することが説明できるのである。
ここまでで光の粒子性について紹介し、光は光子という粒子であると
仮定するといくつかの現象を非常によく説明できるということを紹介した。
それでは光は完全に粒子であるのかというと、それだけでは説明できないこともある。
光の干渉、回折といった現象は波動だと考えないと説明が出来ない。
そこで、「光は波であると同時に粒子でもある」という奇妙な結論を
得ることになった。
以上光の波動性と粒子性について見てきたが、
光だけでなく物質も奇妙なふるまいをすることがわかってきた。
以下では物質について扱う。
原子は原子核の周りに電子が回っているという構造をしている。
これは中学でも習うはずなので、広く知られていることだろう。
しかし、月が地球の周りを回るように電子が原子核の周りを
回っていると考えると問題が起こる。
古典電磁気学によると、加速度運動をする荷電粒子は
電磁波を放出するはずである(円運動は加速度運動である)。
すると電子は運動エネルギーを失い、
原子核に墜落してしまう。
実際に計算してみると、電子が原子核に墜落する速さは
10[cm/s]程度と非常に速い。
原子の大きさは10−10[m]程度である。
このことを考えると、原子が安定して存在していることが
説明できなくなってしまう。
この問題に対し、ボーアはエネルギー量子仮説をふまえ、
原子のエネルギーも離散的な値しかとらないのではないかと
考えた(このようにエネルギーなどの物理量が離散的な
値しかとらないことを「量子化されている」と言う)。
そう考えると原子のエネルギーは最小単位以下の値を
とることが出来ず、電子が墜落することはなくなる。
原子のとりうる離散的エネルギーをエネルギー準位と呼ぶ。
原子のエネルギー準位は不連続なので、
エネルギーの変化は不連続になる。
このことから、原子の放射する光はいつも同じエネルギーを
持つことになる。 E=ħωから、エネルギーの同じ光は
同じ振動数を持つことになる。
このことにより、原子が特定の振動数の光を発すること
(原子のスペクトル)も説明されることになった。
原子も電磁波と同じようにエネルギーが量子化された。
このことから、ド・ブロイは原子、すなわち物質も波動の性質を
持つのではないかという驚くべき仮説を唱えた。
電磁波が波動であると同時に粒子であるのと同じように、
物質は粒子であると同時に波動であるというのである。
これは突拍子もない考え方であったが、
何と実験で物質が波動であると考えないと説明できない現象が
見つかったのである。
これについては、次節で扱う予定である。
ド・ブロイは、物質のエネルギーと運動量も
電磁波と同じE=ħω、p=h/λという関係を持つと考えた。
よって、波動としての物質の持つ波長は
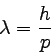 |
… (4) |
ということになる。
これはド・ブロイ波長と呼ばれる。
量子力学とは、このような波動としての物質(物質波、ド・ブロイ波)が
どのように振舞うかを考えていく分野である
(粒子としての電磁波に関する分野は量子光学と呼ばれる)。
次節以降では、物質波の解釈や物質波の従う方程式(シュレディンガー方程式)の
説明をしていく予定である。
|
|
