前節では、光の粒子性について触れた。
光は確かに粒子性があるのだが、
光子1つのエネルギーは非常に小さいため
それまでは発見されなかったのである。
光に粒子性があるのと対応して
物質にも波動性がある。
この節では、物質の波動性を見る干渉実験を紹介する。
量子力学では物質の波動性と粒子性について扱うが、
粒子と波動の違いが良くわかる実験を見てみよう。
まず粒子について、以下のような装置を考える。
 |
… (a) |
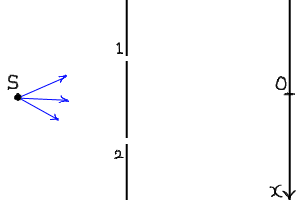
Sから粒子が次々に右側に飛び出すとする。
ただし、飛び出す粒子はまっすぐ右側に飛び出すのではなく、
毎回ある程度違った方向に飛び出す。
例えば、図の青い矢印で示した方向に飛びうるとする。
図の真中にあるのはついたてであり、2つのスリットが
開いている。
Sから飛び出した粒子はスリット1または2を通って
図の右端まで到達することが出来る。
右端にはスクリーンを用意しておき、粒子がどこに達したかを
記録しておくようにする。
まずスリット2を閉じて実験を開始することを考えてみよう。
すると、粒子はスリット1を通った場合のみスクリーンに到達するので、
Sとスリット1を結ぶ直線付近に粒子が到達することがわかる。
一方スリット1を閉じると、今度はSとスリット2を結ぶ
直線に近い軌道を描くことになる。
スリットを両方開けた場合は、スリットを片方閉じた
場合の足し合わせになると考えられる。
粒子はスリット1または2のどちらか一方を通るので、
単純な足し算で考えてよいわけである。
スクリーン上のある点に到達した粒子の中で
スリット1を通ったものの頻度をP1、
スリット2を通ったものの頻度をP2
とする。
すると、スクリーン上のある点に到達した粒子の頻度P12は
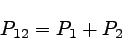 |
… (1) |
という風に表される。
Sから粒子が飛び出す方向がランダムだとすると、
頻度P1、P2、P12は
粒子がある点に到達する確率であると考えることが出来る。
よって、以下ではこれらが確率を表すと考えることにする。
P1、P2、P12を図示すると
以下のようになる。
 |
… (b) |
グラフの上側は、P1、P2、P12の
xに対する分布を表している。 スリット1を通った粒子は図(a)の上側に到達する
確率が高く、スリット2を通った粒子は図(a)の下側に到達する確率が高い。
このことを表しているのが図(b)の黒い線である。
一方、赤い線はP12を表している。
これは黒い線の値を重ね合わせたグラフになっている。
図(b)の下段はスクリーンに実際に粒子が当たる様子で、
赤いグラフに対応している。
赤色が濃いほど粒子が到達しやすいことを表している。
さて、今度はSから波が発生する場合スクリーンにどのように
到達するのかを考えてみよう。
波動は一般に振幅をA、位相をθとしてA cosθと書けるが、
ここでは計算を簡単にするためAeiθ(=φと置く)という表現を使うことにする。
オイラーの公式を使うとeiθはcosθ+i sinθと書けるので、
実数部分が実際の波を表すことになる。
Sから球面波が発生する場合、
スリット1及び2を通った波は以下のようになると考えられる。
 |
… (c) |
青はスリット1を通った波で、赤はスリット2を通った波である。
ここでは見やすくするために色を変えたが、
緑、赤、青で波の性質は全く変化していない。
粒子の場合と同じように、スクリーンに到達する波の頻度を考えてみよう。
波の場合は頻度をその点の振幅の自乗で考えると良いだろう。
波の式はφ=Aeiθであるので、
|φ|2がちょうど振幅の自乗A2を表すことになる。
よって、スリット1を通った波と2を通った波のスクリーンにおける頻度は
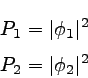 |
… (2) |
と表すことが出来る。
スリットを両方開けた場合、
これらの波は干渉を起こし、強め合うところと弱めあうところが
発生する。
すると、全体の頻度P12は単純にP1と
P2を足したものではなくなる。
干渉を考える場合、まず波の式φを足し合わせて、
その後自乗しなければならない。
よって、Sで発生した波のスクリーンに到達する頻度は
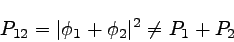 |
… (3) |
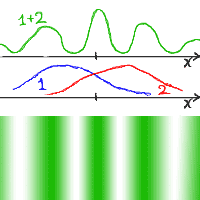
となる。 この様子は、図示すると以下のようになる。
 |
… (d) |
上側の2つのグラフは、到達する波の頻度を表している。
青いグラフはスリット2を閉じて1からだけ通した時のもので、
赤は逆にスリット2のみを通ったときのものである。
ここまでは粒子の場合でも波動の場合でも大きな違いは現れていない。
緑色は両方を開けたときのもので、強め合うところと弱めあうところがあるので
両方のグラフを単に足しただけのものにはなっていない。
下段は先ほどと同じように、頻度の高い部分を濃い色で表した図である。
粒子の場合とは違って、波動の場合は縞模様(干渉縞)が現れることがわかる。
以上は粒子と波の違いを表す実験であった。
ここから量子力学に入る。
物質は粒子であると信じられてきたが、ド・ブロイにより
物質も波動の性質を持つのではないかという説が考え出されたということは
前節で紹介した。
そこで、実際に物質を使ってこの実験をするとどうなるのか見て行こう。
ここでは、電子を例にとって考える。
Sから電子を右側に打ち出し、スクリーンにどのように到達するかを調べて
電子が粒子であるのか波動であるのかを考えるわけである。
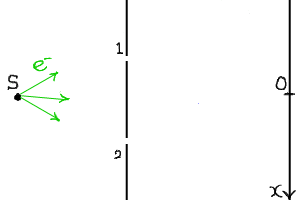
装置は以下のようなものになる。
 |
… (e) |
まず、電子はいくつあるか数えることが出来るので確かに粒子の性質を持っている。
しかし、実際に実験をしてみると何と干渉縞が現れるのである!
すなわち、電子の分布はこのようになる。
 |
… (d) |
これは、電子を同時にたくさん打ち出した場合にそれらが衝突して
起こっているのではない。
電子を1つ打ち出し、スクリーンに到達したことを確認してから
次の電子を打ち出すということを繰り返し、
スクリーン上で到達した電子の数を計測すると縞模様の頻度分布になっているのである。
電子をはじめとして物質は、このような波動性をもっているということが判明した。
しかしこれが結局どういうことなのか(この波が何なのか)
はいまだに良くわかっていない。
まず考えられるのは、電子が純粋に波動であるということだが、
そうすると物質同士が衝突することも説明できなくなる。
このように、物質は光と同じく「粒子であると同時に波動」なのである。
この実験では電子を用いているが、電子は非常に小さい。
一方、ある程度の大きさを持ったもの(ボールなど)でこの実験を行うと、
波動としての性質は全く示さない。
このように、量子力学の性質は非常に小さい、ミクロなスケールに
おいて成り立っているのである。
電子も干渉を起こすので、両方のスリットを開いたときの頻度分布
P12はP1+P2になっていない。
そこで、電子においても波の式に対応する量が必要になる。
電子における波の式は確率振幅と呼ばれ、ここではφと表すことにする。
確率振幅はφ=Aeiθという風に表される複素数であり、
確率「振幅」と表現するが振幅Aだけでなく波の式自体を表すものである。
電子の確率分布は、確率振幅をφとして上の(2)式のように表されることになる。
確率振幅自体は複素数で、何か(観測できる量)を表す量ではない。
その絶対値の自乗をとると(2)式のように確率を表すようになる量である
(電子は純粋に波動であるわけではないので、最初に扱った粒子の実験と
同じようにその頻度は確率を表す)。
電子には波動性があるようだが、この実験で両方のスリットを開けた場合、
電子はどちらかを通っていると言えるのかどうかという問題がある。
粒子の場合は必ずスリット1かスリット2のどちらか一方を通っている。
一方、波動は両方を通るため干渉を起こす。
粒子性と波動性の両方を持つ電子はどうだろうか?
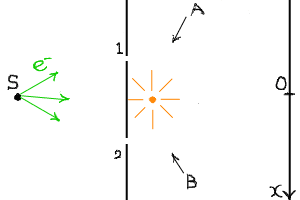
このことを考えるために、装置を以下のように改造してどちらの
スリットを通るのかを考えてみよう。
 |
… (f) |
中央のオレンジ色のものは光源である。
AとBの方向から光を観測していれば、
光がさえぎられることがあったかどうかでスリット1を通ったか2を通ったか知ることが出来る。
この実験を実際にやってみると、確かにスリット1か2のどちらかを
通っていることがわかる。
電子1つにつき確かに1回AまたはBで光源がさえぎられることが観測され、
両方同時に光がさえぎられることはない。
それでは、スリット1か2のどちらか一方を通過しているのに
電子は干渉を起こしているのだろうか?
実はそうではない。
光源を設置して実験を行ってスクリーンの様子を調べると、
干渉縞がなくなるのである!
光源を設置したことにより、以下のような粒子の性質のみの状態に
なってしまうのである。
 |
… (b) |
電子が粒子でしかないのならば片方のスリットしか
通らないのはあたりまえである。
このようにスクリーン上の電子の分布が変化してしまった理由は、
光源を設置したことにある。
光源から発生した光は電子に当たると、電子の状態に影響を
与えてしまうのである。
スリット1か2かどちらを通ってきたかわかった電子は、
もはや干渉は起こさない。
このように、量子力学では観測するという行為が
対象に影響を与えてしまうという不思議な現象がある。
これは不確定性原理の一例であると言われている
(不確定性原理についてはいくつか考えるべき問題があるので、
別の節で改めて扱いたいと思っている)。
電子の干渉実験において、実験に影響を与えたのは光源であり、
観測という行為自体ではない。
人間が見ているか見ていないかによって
電子の状態が変化するのではないことに注意しなければならない。
原理的に観測できる状態になっているかなっていないかだけが問題なのである。
観測が状態に影響を与えるということについて、
人間の意識に関係があるとしばしば誤解されているが、
ここで見たようにそれは間違いである。
結局、電子の干渉が起こるときに電子はどちらかのスリットを通っているのか、
それとも両方を通っているのかについては決着はついていない。
ただ、どちらであるかを観測することは不可能であるということは
わかっているのである。
そこで多くの場合、これは考えても仕方がない問題だとされている。
ここまでで物質の波動性を示す干渉実験を見てきた。
これに関連して、量子力学で使われるブラ・ケット記法について
紹介しておこう。
量子力学で使われる確率振幅は、以下のように括弧を使って表される。
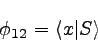 |
… (4) |
φ12は電子の干渉実験のところで出てきた、
両方のスリットを開いたときの確率振幅である。
左が今までの記法で、右がブラ・ケット記法である。
Sは電子の飛び出した時の状態を表し、xはスクリーンに達したときの状態を
表している。 Sからスリットを経てスクリーン上のあるxという点に
達するということを上記のように表すのである。
つまり、確率振幅をブラ・ケットで表した場合、右から左に読んでいくことになる。
このように括弧(bracket)で表されるためブラ・ケットと呼ばれている。
何故ブラケット記法ではなくブラ・ケット記法と言うのかというと、
ブラとケットは分離できるからである。
上の例では、|S>をケット・ベクトル、<x|をブラ・ベクトルと言う。
何故ベクトルと呼ぶのかに関しては次節で具体例を示しながら説明していく予定である。
ブラおよびケットは状態を表す量で、状態ベクトルとも呼ばれる。
例えば|S>は、Sから放出された電子の状態を表していることになる。
確率振幅<x|S>は、状態Sから状態xにいたる振幅である。
|S>を状態「ベクトル」と呼ぶのに対して
<x|S>自体は複素数のスカラー量であることには注意が必要だ。
確率振幅φ1(スリット2を閉じて1からだけ電子を通したときの振幅)
もブラ・ケット記法で表してみよう。
この場合は電子はSから発せられ、スリット1を経由し、
スクリーンに到達する。
このような場合の確率振幅は以下のように表す。
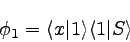 |
… (5) |
Sから1にいたる振幅と1からx(スクリーン)にいたる振幅が
掛け合わされている。
このように、ある状態とある状態が同時に起こる場合、その確率振幅は
掛け算で表される。
全体の確率振幅はそれぞれのスリットを通る場合の
確率振幅の和で表されるのであった。
このことをブラ・ケット記法で表すと以下のようになる。
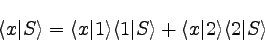 |
… (6) |
これはφ12=φ1+φ2を
書き直したものである。
このように、二つの状態のどちらかが起こるという場合、
確率振幅は足し算で表されることになる。
確率振幅は複素数なので、自乗してから足すのと
足してから自乗するのでは違う結果が出る。
量子力学では確率を足すと全体の確率になるのではなく、
振幅を足して自乗することによって全体の確率を求めるのである。
この節では粒子の波動性を紹介し、量子力学の記法を導入した。
次節では具体例を用いてこれらの記法をさらに説明する予定である。
|
|
