�������Ǥ�����ˤҤ��ĤŤ��̻��ϳؤδ���Ū��ʬ�������
�äˣ����ַϡʣ���̷ϡˤ���ˤȤꡢ
���֥٥��ȥ롢ʪ���̤ȱ黻�ҡ����֤λ���ȯŸ���������롣��
��Ⱦ�Ǥϣ����ַϤζ�����Ȥ��ƥ˥塼�ȥ�ο�ư������
���������˥塼�ȥ�Τ˴ؤ���ܤ��������ϹԤ�ʤ�����
�������Ϥ�λ������������������
��������Ͽ�����¿�������ʤ�Ĺ���ʤäƤ��ޤä���
�����������줾��ο������ΤϷ褷�����ʤ��Ȼפ��Τǡ�
���Ȥ���ĥ�äƺǸ�ޤ��ɤ�Ǥ���������������
������Ǥ�ʪ������ư�������ļ¸���Ҳ𤷡�
�֥顦���åȵ�ˡ��Ƴ����������
�֥�ڤӥ��åȤϾ��֥٥��ȥ�ȸƤФ��ΤǤ��ä�����
�����ǤϤޤ��ɤ����ƾ��֥֡٥��ȥ�פȸƤФ��Τ��Ȥ������Ȥ���ͤ��Ƥߤ褦����
������κǸ�ǡ��Ӥ������ӽФ����ŻҤ�����������ã����Ȥ���
��Ψ�����ϰʲ��Τ褦��ɽ�����Ȥ������Ȥä�����
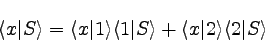 |
�������ġ��ʣ��� |
���μ��Ƥߤ�ȡ��٥��ȥ�����Ѥη��ˤʤäƤ��뤳�Ȥ�
���Ť��ʤ�������������
���ʤ�����ʲ��Τ褦�ʼ��ȡʣ��˼������Ƥ���Ȥ������ȤǤ��롣��
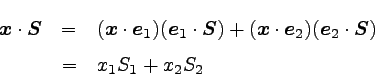 |
�������ġ��ʣ��� |
�ã���ȡã��������ñ�̥٥��ȥ���ȹͤ���ȡ�
�Τ��ˡʣ��ˤȡʣ��ˤ�Ʊ�����ˤʤäƤ���ȹͤ����롣��
���ξ��ϡ����֡ãӡ�ȡã���Ρã�����ʬ�ȡã�����ʬ����Ф��ƹͤ��Ƥ���
�Ȥ������Ȥˤʤ롣��
�����Τ褦�ˡ��̻��ϳؤǤϾ��֤�٥��ȥ��ɽ�����롣��
����Ū�ˡ��̻��ϳؤˤ�������֤Ϧסʥץ����ˤȤ������ꥷ��ʸ����
�Ȥä�ɽ�����Ȥ�¿������
���֦פ�ɽ�����֥٥��ȥ�ϡæס�Ȥ������Ȥˤʤ롣��
�����ؤˤ����ơ��٥��ȥ�Ȥ�����μ��Τ����Ū���̤Ǥ��롣��
�������������ɸ�Ϥ����ꤷ�ƥ٥��ȥ����ʬ��ºݤ˽Ф��Ƥߤ��
�狼��䤹���ʤ롣��
�����Ʊ���褦�ˡ����֥٥��ȥ���ɸ�Ϥ����ɽ������Ȥ狼��䤹���ʤ롣��
�̻��ϳؤˤ����ơ���ɸ�Ϥδ���٥��ȥ�ʣ������Υǥ���Ⱥ�ɸ�Ǥϣ���������������
���������б��������Ū�ʥ٥��ȥ�ˤȤʤ���֥٥��ȥ��
�ִ��ܾ��֡פȸ�������
���ܾ��֤��̾�κ�ɸ�Ϥδ���٥��ȥ��Ʊ���褦��
�礭�������ˤʤ�褦�����ꤷ�Ƥ�������
�ޤ����ۤʤ���ܾ���Ʊ�Τ����Ѥϥ����ˤʤ�褦�ˤ��Ƥ�������
���ºݤ�ʪ���Ϥˤ����ƴ��ܾ��֤ϤɤΤ褦�ʤ�Τ�����������
�㤨�Ф����Ĥ�γ�Ҥα�ư�ˤĤ��ƹͤ��롣��
����ȡ�����γ�Ҥξ��֤�̵���ˤ��ꡢͭ�¼����Υ٥��ȥ�Ǥ�ɽ���ʤ����Ȥ��狼�롣��
���Τ褦�ˡ����̤ˤϾ��֥٥��ȥ��̵�¼����Υ٥��ȥ�Ǥ��롣��
��äơ����μ�갷�����̾�ֺ�ɸɽ���פȤ�����ˡ���Ѥ��ƹԤ��롣��
����ˤĤ��Ƥϼ���Ǽ��夲��ͽ��Ǥ��롣��
�����̤�ʪ��Ū�ʾ��֤�̵�¤ˤ��뤬��
���Ū��ͭ�¸Ĥξ��֤�����Ǥ����礬���롣��
������ϸ�ۤɵ뤬��
�����ǤϾ��֡ã���Ⱦ��֡ã������ܾ��֤Ȥ���
�������ηϤ�ͤ��롣��
���Τ褦�ʷϤϣ����ַϤȸƤФ�롣��
�������ַϤδ��ܾ��֡ã���ȡã�������Ū����ʬɽ�����Ƥߤ褦����
�����Ϻ�ɸ�Ϥˤ��������٥��ȥ��Ʊ���ʤΤǡ�
�ʲ��Τ褦��ɽ�����Ȥ��Ǥ��롣��
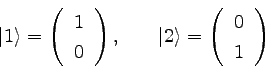 |
�������ġ��ʣ��� |
���åȥ٥��ȥ�æס���̾盧�Τ褦�˽ĥ٥��ȥ��ɽ����롣��
������Ф��֥�٥��ȥ��סäϰʲ��Τ褦�˲��٥��ȥ��ɽ����롣��
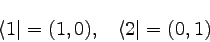 |
�������ġ��ʣ��� |
���̤ˡ��֥�ϥ��åȤ٥��ȥ�ˤ���ʣ�Ƕ����Ȥä����
������������Ѹ�Ǹ����ȥ���ߡ��ȶ���ˤ�ɽ������
���֥饱�åȡ�סæա�Ͼ��֥٥��ȥ�Ʊ�Τ����Ѥ�ɽ������
���٥��ȥ�߽ĥ٥��ȥ�Ȥ������ˤʤꡢ�̾�ι���α黻��
�Ԥ��Ф褤���Ȥˤʤ롣��
���ѡ�סæա����������������̤��Ψ������ɽ�����Ȥˤʤ롣��
��Ψ�����ϰ��̤�ʣ�ǿ����ä��Τǡ����֥٥��ȥ�γ���ʬ��
ʣ�ǿ��Ǥ��ɤ��Ȥ������Ȥ��狼�롣��
���ʣ��ˡ��ʣ��˼���ɽ�������֡ã��䡢�ã�������Ѥ�ºݤ˼�äƤߤ��
�ʲ��Τ褦�ˤʤ롣��
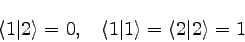 |
�������ġ��ʣ��� |
���֣��Ⱦ��֣������Ѥϥ����ˤʤäƤ��롣��
����Ͼ��֣��Ⱦ��֣���ľ�Ƥ����ɽ�����롣��
���֣�Ʊ�Τ����ѤȾ��֣�Ʊ�Τ����Ѥϣ��ˤʤäƤ��롣��
�̾�Υ٥��ȥ��Ʊ���褦�˼�ʬ���Ȥ����ѤϤ��Υ٥��ȥ��
�礭���μ����ɽ���Τǡ������Υ٥��ȥ���礭���ϣ��Ǥ��롣��
�̻��ϳؤˤ�������֥٥��ȥ�ϡ�����礭�������ˤʤ�褦��
���Фʤ���Фʤ�ʤ�����
���֥٥��ȥ���礭�������ˤʤ�褦��Ĵ�����뤳�Ȥ�
�ֵ��ʲ�����פȸ�������
�����֥٥��ȥ�ʲ�������ͳ�ϡ����֥٥��ȥ�γ���ʬ��
��Ψ������ɽ������Ǥ��롣���㤨�Ф�����֡æס��
�裱��ʬ�ϡ㣱�æס�Ƚ��Ȥ��Ǥ������֦פ����֣��Ǥ���
��Ψ������ɽ������
�������裲��ʬ�Ͼ��֦פ����֣��Ǥ����Ψ������ɽ������
��Ψ�����Ϥ��μ��褬��Ψ�ˤʤ�Τǡ�
��Ψ�����μ�������¤�����Ψ�������������ˤʤ�ʤ���Фʤ�ʤ�����
���Τ褦����ͳ�ǡ����֥٥��ȥ�γ���ʬ�μ�������¡����ʤ��
���֥٥��ȥ���礭���μ���ϣ��ˤ���ɬ�פ����롣
������������֡æס䤬�ʲ��Τ褦�ʾ��֤Ǥ���Ȥ��롣��
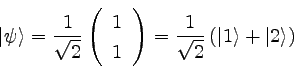 |
�������ġ��ʣ��� |
�ޤ������ξ��֤ϵ��ʲ�����Ƥ���ΤǾ��֥٥��ȥ�Ȥ���Ŭ�ڤǤ��뤳�Ȥ��狼�롣��
���ξ��ˡ����ξ��֦פȾ��֣��ڤӣ��Ȥ����Ѥ���Ƽ��褹���
�ʲ��Τ褦�ˤʤ롣��
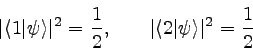 |
�������ġ��ʣ��� |
���Ѥϳ�Ψ������ɽ������Ψ�����μ���ϳ�Ψ��ɽ���ΤǤ��ä�����
�ʣ��˼��ˤ��ȡ����֦פ����֣��Ǥ����Ψ��������
���֣��Ǥ����Ψ����������Ȥ������Ȥˤʤ롣��
����Ϥɤ��������Ȥ�����������
�ºݤ˦פȤ���ʪ�����֤��¸����Ƥ���Ȥ��ˡ�
���֡ã��䤫�ã���Τɤ����ȤäƤ���Τ���¬�ꤷ���Ȥ��롣��
����ȡ�¬���̤ϣ�����γ�Ψ�Ǿ��֣���������γ�Ψ�Ǿ��֣��ˤʤ�ΤǤ��롣��
�æס�Ȥ������֤������˺Ƹ�����Ƥ⡢
¬�ꤹ�뤿�Ӥˤ��η�̤��㤤����ΤǤ��롪��
���Τ褦��ʪ�����֤˳�ΨŪ�����ʤ�����Ȥ������Ȥ�
�̻��ϳؤ������礭����ħ�Ǥ��롣��
���ʣ��˼��ξ��֦פ��Ф��ơ�����¬���Ԥä��Ȥ������֣��Ǥ��ä��Ȥ��롣��
����ľ�塢�⤦����¬���Ԥ��Ȥɤ��ʤ������������
���֣������Ȥ⣵����γ�Ψ��¬�ꤵ��뤳�Ȥ�ͽ�ۤ���뤬��
���ξ��ˤ�¬���̤�ɬ�����֣��ˤʤ롣��
���֦פϴ�¬������̾��֣����Ѳ����Ƥ��ޤä��ΤǤ��롪��
���Τ褦�ˡ�¬��ˤ����֤��Ѳ����Ƥ��ޤ�����Τ��Ȥ�
�ִ�¬����פȸ�������
��¬����ϸ��ߤǤ�Ϥä���Ȥ������ʤ���Ƥ��ʤ���
�̻��ϳؤ�̤�������Ǥ��롣��
�������ޤǾ��֥٥��ȥ�ˤĤ��ư��ä��������������
ʪ���̤��ɤΤ褦��ɽ����뤫��ͤ��롣��
ʪ�����֤����֥٥��ȥ��ɽ�����Τ��Ф��ơ�
ʪ���̤ϱ黻�Ҥ�ɽ����롣��
�黻�ҤȤϡ����֥٥��ȥ�˺��Ѥ����̤Υ٥��ȥ��
�Ѳ��������ΤǤ��롣��
���֤ϴ��ܾ��֤��Ѥ���ɽ���Ǥ��뤬��
�黻�ҤϹ����Ȥä�ɽ�����뤳�Ȥ��Ǥ��롣��
�����ַϤǤϡ����֥٥��ȥ�ϣ������Υ٥��ȥ�ˤʤ�Τǡ�
�黻�Ҥϣ��ߣ������ɽ����뤳�Ȥˤʤ롣��
���黻�Ҥ���Ȥ��ơ����ͥ륮�����б�����ϥߥ�ȥ˥���Ȥ���
�黻�Ҥ�ͤ��Ƥߤ褦����
�ϥߥ�ȥ˥�����̾�Ȥ�ɽ����롣��
�Ȥ��黻�ҤǤ��뤳�Ȥ�Ĵ���뤿��ˡ��Ȥξ�ˡ��ʥϥåȡˤ�
�失��ɽ�������礬¿���ʻ�ǰ�ʤ���ȣԣ̤ͣ�ɽ��������ˡ�����Τ�ޤ���ġˡ�
�������ϥߥ�ȥ˥��ʲ��Τ褦�ˤʤäƤ��������ͤ��롣
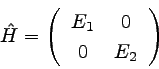 |
�������ġ��ʣ��� |
�������������ȣ����ϰۤʤ�¿��Ǥ���Ȥ��롣��
�ϥߥ�ȥ˥������֣��ڤӾ��֣��˺��Ѥ��������ɤΤ褦��
�ʤ뤫������Ƥߤ�ȡ�
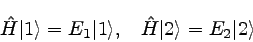 |
�������ġ��ʣ��� |
�Ȥʤ롣���黻�Ҥ�٥��ȥ�˺��Ѥ�������̡��ɤ���ξ���
����߸��Υ٥��ȥ뤬ɽ��Ƥ��롣��
���Τ褦�ʥ٥��ȥ������Ϲ���˸�ͭ�Τ�Τǡ�����������Ѹ��
��ͭ�ͤȸ�ͭ�٥��ȥ�ȸƤФ�롣��
�ϥߥ�ȥ˥���ϥ��ͥ륮����ɽ���黻�ҤʤΤǡ�
�ä˥ϥߥ�ȥ˥���θ�ͭ�٥��ȥ�ͥ륮����ͭ���֡�
��ͭ�ͤͥ륮����ͭ�ͤȸƤ֡���
�����ͥ륮����ͭ���֤ˤ����ƥ��ͥ륮����¬�ꤹ��ȡ�
ɬ���б����륨�ͥ륮����ͭ�ͤ������롣��
���ξ��Ǥϡ����֡ã���Ǥ��뤳�Ȥ��狼�äƤ�����֤ǥ��ͥ륮����¬�ꤹ���
�����ͤ�ɬ�������Ȥʤ�ΤǤ��롣��
�����Τ褦�˴��ܾ��֤����ͥ륮����ͭ���֤ˤʤäƤ���Ȥ���
�ϥߥ�ȥ˥����гѲ�����Ƥ���פȸ�������
�ºݤ˴�¬����륨�ͥ륮���ϥ��ͥ륮����ͭ�ͤǤ���Τǡ�
�ϥߥ�ȥ˥�������������μ�ˡ�ˤ����гѲ����뤳�Ȥ�
�̻��ϳؤν��פ�����ˤʤ롣��
������Ǥϥ��ͥ륮����ͭ���֤Ǥʤ����֤ǥ��ͥ륮����¬���
�Ԥ��Ȥɤ��ʤ������������
�����륨�ͥ륮�����ͤϡ�ɬ�����ͥ륮����ͭ�ͤΤɤ줫�ˤʤ�ΤǤ��롣��
���ξ��ϥ��ͥ륮����¬���̤�ɬ�������������ˤʤ�ΤǤ��롣��
�����������ͥ륮����ͭ���֤Ǥʤ����֤Ǵ�¬��Ԥ��ȡ�
�ɤ���Υ��ͥ륮���ˤʤ뤫�ϳ�Ψ�ˤ�ä�ɽ����뤳�Ȥˤʤ롣��
¬�ꤵ��륨�ͥ륮���δ����ͤϡ����֥٥��ȥ�DZ黻�Ҥ�Ϥ���Ƿ����뤳�Ȥˤ�ä������롣��
�㤨�Сʣ��˼��ξ��֡æס�ˤ����륨�ͥ륮���δ����ͤ�
�ϥߥ�ȥ˥���ʣ��˼���Ȥä�ɽ���Ȱʲ��Τ褦�ˤʤ롣��
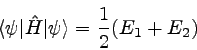 |
�������ġ��ʣ����� |
��ۤɵ���̤Ǥϡ����֡æס䤬���֡ã���Ǥ����Ψ�ϣ�����
���֡ã���Ǥ����Ψ�ϣ�����Ǥ��ä�����
��äơ����ͥ륮��������ˤʤ��礬������
�����ˤʤ��礬������γ�Ψ�Ǽ¸�����ΤǤ��롣��
���Τ褦����ͳ�ˤ�ꡢ�����ͤϡʣ����˼��Τ褦��ɽ�����ΤǤ��롣��
�����ˡ����֥٥��ȥ뤬�ɤΤ褦�˻����Ѳ����뤫��ͤ��褦����
���֤λ���ȯŸ�ˤϥϥߥ�ȥ˥���̩�ܤ˴ط����Ƥ��롣��
�����Ϥϡ����ޤǤ�Ʊ�������ܾ��֤��ʣ��˼���ɽ����룲���ַϤǤ��롣��
�ϥߥ�ȥ˥���ϡʣ��ˤ�ɽ�����Ȥ��롣��
�����֤ϻ��֤��ФĤˤĤ��Ѥ�ꤦ��Τǡ����֥٥��ȥ�ϰ��̤ˤ�
���֤δؿ��ˤʤ�ʥ����ǥ��������ξ��ˡ���
�����ǡ����֤δؿ��Ǥ�����֥٥��ȥ��æ��ʣ��ˡ�ʥץ�������ʸ���ˤȤ�������
���֦��ϻ��֤ˤ�ä��Ѳ�����Τǡ����줾�����ʬ����֤ˤ�ä��Ѳ������
�ͤ����롣����������ʬ��ʲ��Τ褦��ɽ�����Ȥˤ��롣��
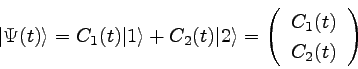 |
�������ġ��ʣ����� |
�����������֥٥��ȥ�ϻ��֤˴ط��ʤ����ʲ�����Ƥ��ʤ���Фʤ�ʤ�����
���Τ���ˤϡ���ʬ�����ȣ������ʲ��ξ���������ɬ�פ����롣��
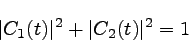 |
�������ġ��ʣ����� |
�����֥٥��ȥ뤬�����Ѳ������硢
���ξ��֥٥��ȥ�ϰʲ��μ��˽��äƻ����Ѳ����롣��
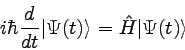 |
�������ġ��ʣ����� |
����ϥ����ǥ����������ʰ��̷��ˤȸƤФ���̻��ϳؤ�
����Ū���������Ǥ��롣��
���ߤǤϥ����ǥ������������̻��ϳؤθ����Σ��ĤǤ���ȹͤ����Ƥ��ꡢ
¾�Τ�Τ���Ƴ�����ȤϤǤ��ʤ��ʿ�¬���뤳�ȤϤǤ��뤬�ˡ���
�����֥٥��ȥ�ʣ����ˤ��ǥ�������������������ȡ�
����ʬ���Ф��룲�Ĥ���ʬ�������������롣�����������ϥߥ�ȥ˥����
�ʣ��ˤΤ�ΤΤޤȤ�����
�������������ϰʲ����̤�Ǥ��롣
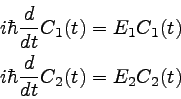 |
�������ġ��ʣ����� |
�����Ϥ��줾����Ω������ʬ�������ǡ��ѿ�ʬΥˡ��ȤäƲ���ñ�˵��뤳�Ȥ��Ǥ��롣��
��̤ϰʲ��Τ褦�ʤ�ΤǤ������ʬ�������β������Τ�ʤ�����
��������ʬ���������������Ʋ�ˤʤ뤳�Ȥ��ǧ������ɤ��ˡ���
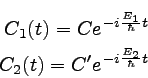 |
�������ġ��ʣ����� |
�ä���ӣáǤ�Ǥ������Ǥ��롣��������ᣰ�Ǥη������ͤ�����ʣ��ˤ����
�����ʣ��ˤȤ���ȡ����֥٥��ȥ�æ��ʣ��ˡ��
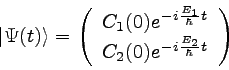 |
�������ġ��ʣ����� |
�Ƚ롣��
�⤷���ᣰ�Ǿ��֡ã�����ä���硢�Ĥޤ�����ʣ��ˡᣱ��
�����ʣ��ˡᣰ�ξ�硢�æ�����裲��ʬ�ϻ��֤��ФäƤ⥼���ΤޤޤǤ��롣��
�裱��ʬ���Ѳ����뤬���ġʥǥ륿�ˤ�¿��Ȥ��ơ������Ѳ��ϣ�����Ȥ������Ƥ��롣��
��Ψ�������Τ�ľ��ʪ��Ū�ʰ�̣���äƤ��餺�������礭���μ��褬��Ψ�ˤʤ롣��
������������ͤ���Ⱦä��Ƥ��ޤ����ҤʤΤǡ�
�¼�����֤��Ѳ����Ƥ��ʤ����Ȥˤʤ롣��
���Τ褦�ˡ��������ˤ����ƥ��ͥ륮����ͭ���֤ˤ����硢
���ηϤξ��֤ϻ����Ѳ����ʤ�����
���ʣ����˼��γ���ʬ�Ϥ��줾�쿶ư���ء�š�ħ�ǿ�ư����ȹͤ��뤳�Ȥ��Ǥ��롣��
����ϥɎ��֥����β���š�ħ�ؤ��б����Ƥ�������狼�롣��
���Τ��Ȥ�ͤ���ȡ����֤λ����Ѳ��˥��ͥ륮����ɽ���黻�ҥϥߥ�ȥ˥���
�ط����Ƥ��뤳�Ȥ������狼��䤹���ʤ����������
�������ǰ������ַϤεƾ��֤λ����Ѳ����ͻҤ�ͤ��롣��
�����ַϤˤϤ����Ĥ��㤬���뤬�������Ǥϥ˥塼�ȥ�Τ��갷�����Ȥˤ��롣��
�˥塼�ȥ�ΤȤϡ���ȿ���κݤ����Ф������γ�Ҥΰ��Ǥ��롣��
�˥塼�ȥ�Τ����ۤ�Ķ�����ˤ�����ȯ�����Ƥ��ꡢĶ�����˥塼�ȥ�Τߥ�����Ǥˤ��
��¬�������ƾ����������Ρ��٥�ޤ���ޤ����Τϵ����˿��������ȤǤ��롣��
�˥塼�ȥ�Τˤ��Żҥ˥塼�ȥ�Ρ��ߥ塼�˥塼�ȥ�Ρ������˥塼�ȥ�Τ�
�����ब���롣��
�����Ϥ��줾���̤�γ�ҤǤ��뤬������˥塼�ȥ�Τ��̤Υ˥塼�ȥ�Τ��Ѳ�����
�֥˥塼�ȥ�ο�ư�פȤ������ݤ�����ΤǤϤʤ����ȸ����Ƥ��롣��
�������Ǥ��ä��Żҥ˥塼�ȥ�Τȥߥ塼�˥塼�ȥ�ΤˤĤ��ƹͤ��롣��
����γ�Ҥ��Żҥ˥塼�ȥ�ΤǤ�����֤�ã��䡢�ߥ塼�˥塼�ȥ�ΤǤ�����֤�
�ã���Ȥ������Ȥˤ��롣��
���줾�����ʬ�Ϻ��ޤǤ�Ʊ���褦�ˡã����ʣ������ˡ��ã����ʣ������ˤȤ��롣��
��������˥塼�ȥ�Τξ��֤Ϥɤμ����γ�ҤǤ��뤫�ˤ�äƤΤߵ��ꤵ���
��ΤǤϤʤ������ɤ��ˤ��뤫���ɤΤ��餤��®�٤DZ�ư���Ƥ��뤫�ʤɤˤ�ä�
���֤�̵�¸�¸�ߤ��Ƥ��롣����������������ˤ��Ƥ���Τ�γ�Ҥ��Żҥ˥塼�ȥ�Τ�
�ߥ塼�˥塼�ȥ�Τ��ɤ���ξ��֤ˤ���Τ��Ȥ������ȤΤߤǤ��롣��
�����ǡ����Ū�ˤ��Υ˥塼�ȥ�Τ��ַϤȤ��ư������Ȥˤ��롣��
�����Υ˥塼�ȥ�ΤΥϥߥ�ȥ˥���ϰʲ��Τ褦�˽�Ȥ��롣��
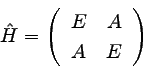 |
�������ġ��ʣ����� |
�Ť���ӣ��ϼ¿��Ȥ��롣��
�ޤ��ǽ�ˡ����֣�����ӣ��ˤ����륨�ͥ륮���δ����ͤ�����Ƥߤ褦����
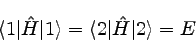 |
�������ġ��ʣ����� |
������Żҥ˥塼�ȥ�Τȥߥ塼�˥塼�ȥ�ΤΥ��ͥ륮���δ����ͤ��Ȥ��
�ŤǤ��뤳�Ȥ�ɽ���Ƥ��롣��
�ºݤΥ˥塼�ȥ�Τ˴ؤ��Ƥ�̤�Τ���ʬ��¿����
���Τ褦�ˤʤäƤ���Τ��ɤ����Ϥ狼�äƤ��ʤ�����
���ϥߥ�ȥ˥������֣�����ӣ��˺��Ѥ�����ȡ��ʲ��Τ褦�ˤʤ롣��
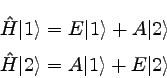 |
�������ġ��ʣ����� |
���ᣰ�ʤ����ۤɤ�Ʊ���褦�ˡ����֣��ȣ��ϥ��ͥ륮����ͭ���֤ˤʤäƤ��롣��
�����������⣰�ξ��Ϥ����ξ��֤ϥ��ͥ륮����ͭ���֤ǤϤʤ�����
�ºݤΥ˥塼�ȥ�Τϡ����������Ǥʤ���ǽ�������뤽���Ǥ��롣��
�˥塼�ȥ�ΤˤϤ����鷺���������̤����뤳�Ȥ���ǧ����Ƥ��롣��
���Τ��ᡢ�˥塼�ȥ�Τξ��֤�¾�ξ��֤νŤ�碌�Ǥ����ǽ�������ꡢ
���ξ����⣰�ˤʤ�ȤΤ��ȤǤ��롣��
�����ơ����֣�����ӣ��ϥ��ͥ륮����ͭ���֤ǤϤʤ��ä��Τǡ�
���ͥ륮����ͭ���֤�õ�����Ȥ��ޤ�����ˤʤ롣��
����ϰ��̤ˤϸ�ͭ�͡���ͭ�٥��ȥ����ƹ�����гѲ���������˵��夹�뤬��
�����ǤϤ⤦������ñ�˥��ͥ륮����ͭ���֤�õ�����Ȥ��Ǥ��롣��
�ʣ����˼����о������顢����飲�Ĥμ���������ΤȰ�������Τ�
��ͭ���֤ˤʤäƤ��뤳�Ȥ���¬�Ǥ��롣��
���ʤ�����ʲ��Τ褦�ˤʤ롣��
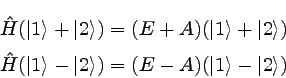 |
�������ġ��ʣ����� |
����飲�Ĥξ��֤��˦����ʥ������ץ饹�ˡ�����
�ʥ������ޥ��ʥ��ˤȤ������Ȥˤ��褦����
�����������֥٥��ȥ�ϵ��ʲ����ʤ���Фʤ�ʤ�����
���ʲ��ޤǹԤ��ȡ����ͥ륮����ͭ���֤Σ��ĤΥ٥��ȥ�ϰʲ��Τ褦�ˤʤ롣��
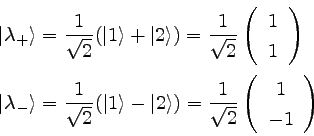 |
�������ġ��ʣ����� |
�����֤δؿ��Ǥ�����֡æ��ʣ��ˡ���ͥ륮����ͭ���֤�Ȥä�ɽ���Ƥߤ褦����
���Υ٥��ȥ�ϡ����֣�����ӣ���Ȥäƽ����ʣ����˼��Τ褦��ɽ����Ƥ���Ȥ��롣��
����ϡ��ʲ��Τ褦�˽�ľ���롣��
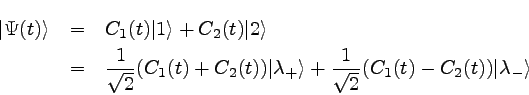 |
�������ġ��ʣ����� |
���Τ褦�ˡ����֦��ͥ륮����ͭ���֤�ɽ�����Ȥ���
�����η����ڤӦ����η����������
�����Ȥ������Ȥˤ��롣��
����Ū�ˤϰʲ��Τ褦�ˤʤ롣��
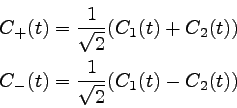 |
�������ġ��ʣ����� |
���ʾ�ǥ��ͥ륮����ͭ���֤��ᡢ�����Ѳ�������֦��ͥ륮����ͭ���֤�ɽ��������
����ǽ����ϴ�λ�����Τǡ������ǥ������������Ѥ���
���֦��λ����Ѳ����ͻҤƤߤ褦����
�����ǥ����������˾��֦��ȥϥߥ�ȥ˥������������
�ʣ����˼���Ȥä���������Ȱʲ��Τ褦���������������롣��
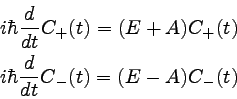 |
�������ġ��ʣ����� |
����Ϥ��줾����Ω������ʬ�������ʤΤǡ�
��ۤɤ�Ʊ���褦���ѿ�ʬΥˡ��ȤäƲ��Ȥ��Ǥ��롣��
��ϰʲ��Τ褦�ˤʤ롣��
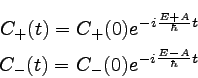 |
�������ġ��ʣ����� |
�����ʣ����˼���Ȥäƣ����ȣ�����ɽ���ȡ�
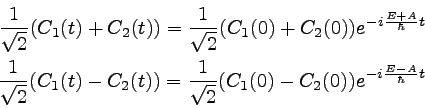 |
�������ġ��ʣ����� |
�Ȥʤ롣��������ϢΩ���ƣ����ʣ��˵ڤӣ����ʣ��ˤ����ȡ�
��̤ϰʲ��Τ褦�ˤʤ롣��
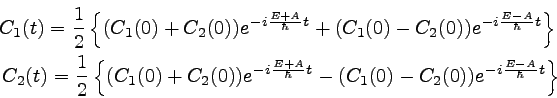 |
�������ġ��ʣ����� |
��������ᣰ�Ǧ������֡ã��䡢���ʤ���Żҥ˥塼�ȥ�Τ��ä��Ȥ��褦����
����ȡ������ʣ��ˡᣱ�������ʣ��ˡᣰ�Ȥʤ�Τǡ�
�����ʣ����˼�����������Ⱦ��֡æ���λ����Ѳ����ͻҤ�
�ʲ��Τ褦�˵����롣��
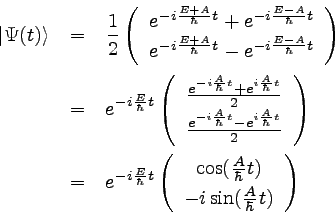 |
�������ġ��ʣ����� |
�����ܤ��飳���ܤη��ˤϥ����顼�θ�����Ȥä�����
���Τˣ�����Ȥ������ΰ��ҡʰ�����ҡˤ������äƤ��뤬��
����������ͤ��ä��Ȥ��ˣ��ˤʤäƤ��ޤ��Τǰ�̣��⤿�ʤ�
�ʤ��������櫓���̻��ϳؤǤ⥨�ͥ륮���δ��Ϥɤ��ˤȤäƤ��ɤ����Ȥˤ�
��ˡ���
��������ʪ��ʪ���ؤʤɤǰ�����Ҥ����˽��פʰ�̣����ľ��⤢��
(�������о������ˤ�)��
�����֦������֣�����ӣ��Ǥ����Ψ�������ᡢ�礭���褹�뤳�Ȥˤ��
���줾��γ�Ψ����Ƥߤ褦����
�ʣ����˼��Τ��줾�����ʬ���礭���μ������Ф褤�Τǡ�
���֣��Ǥ����Ψ����������֣��Ǥ����Ψ������Ȥ���ȡ�
��̤ϰʲ��Τ褦�ˤʤ롣��
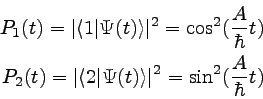 |
�������ġ��ʣ����� |
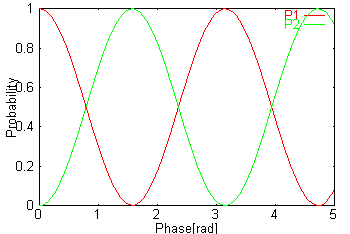
���֤ˤ�äƿ�ư���������줿����
����Ͽ�����Ȱʲ��Τ褦�ˤʤäƤ��롣��
 |
�������ġ��ʣ�� |
�֤��������֣������ʤ���Żҥ˥塼�ȥ�ΤǤ����Ψ�Ǥ��ꡢ
�Ф��������֣����ߥ塼�˥塼�ȥ�ΤǤ����Ψ�Ǥ��롣��
�����ϳ�Ψ�������ϻ��֤�ɽ���Ƥ���ʣ���ħ�Ȥ���ñ�̤���Ѥ����ˡ���
�Żҥ˥塼�ȥ�εڤӥߥ塼�˥塼�ȥ�Τ��ϤΥ��ͥ륮����ͭ���֤Ǥʤ��Ȥ���С�
�������ǥ˥塼�ȥ�Τμ��ब���ꤷ�Ƥ�����Ǥ�
���֤ˤ�ä��̤Υ˥塼�ȥ�Τ��Ѳ�������Ȥ������Ȥ�ɽ���Ƥ��롣��
�����ߡ��˥塼�ȥ�ο�ư�Ϥ��������ʾڵ�
���¤˵����äƤ��븽�ݤ��ȹͤ����Ƥ��롣��
�����ѡ����ߥ�����Ǥʤɤμ¸����ߤˤ�ꡢ����ʤ븦�椬�ʤ�Ǥ��롣
��������Ǥ��̻��ϳؤδ��ä˴ؤ���¿���Τ��Ȥä�����
�ޤȤ��ȡ��ޤ����֤ϥ٥��ȥ��ɽ���졢ʪ���̤ϱ黻�Ҥ�ɽ�����ΤǤ��ä�����
���֤ο��ϰ��̤ˤ�̵�¸Ĥ�����ͭ�¤Ǥ���ȶ���Ǥ�����ˤϴ��ܾ��֤�����
�ºݤ˾��֥٥��ȥ����ʬ��Ф����黻�Ҥ�����ɽ�����Ȥ��Ǥ��롣��
�����Ѳ���ͤ����硢�ޤ��ϥߥ�ȥ˥�����гѲ����ƥ��ͥ륮����ͭ���֤�
õ���������ǥ������������Ѥ��ƻ����Ѳ����ͻҤ뤳�Ȥˤʤ롣��
�����ᤫ��ϡ����������֤�ư����γ�ҤˤĤ��ư�������
���٤Ͼ��֤�ͭ�¸ĤǤϤʤ��Τǡ�����Τ褦�˹���η��˵��夷�ʤ�����
�����ǡ����ܾ��֤Ȥ���γ�Ҥΰ��֤����ֺ֡�ɸɽ���פ�Ȥ����Ȥˤʤ롣��
|
|
